练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

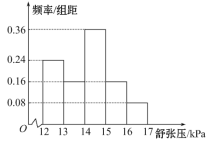
    【题目】为研究某药品的疗效，选取若干名志愿者进行临床试验，所有志愿者的舒张压数据（单位：）的分组区间为，，，，，将其按从左到右的顺序分别编号为第一组，第二组，......，第五组.如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有人，第三组中没有疗效的有人，则第三组中有疗效的人数为( )

    A. B. C. D.

    【答案】C

    【解析】

    由频率分布直方图得第一组与第二组的频率和为0.4，再由第一组与第二组共有20人，求出样本总数n＝50人，由第三组的频率为0.36，求出第三组共有18人，由此能求出第三组中有疗效的人数．

    由频率分布直方图得第一组与第二组的频率和为：1﹣（0.36+0.16+0.08） 1＝0.4，∵第一组与第二组共有20人，

    ∴样本总数n＝＝50人，∵第三组的频率为0.36，∴第三组共有：50×0.36＝18人，

    ∵第三组没有疗效的有6人，∴第三组中有疗效的人数为：18﹣6＝12人．

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在数列{an}中，已知a1=2，an+1=3an+2n﹣1．
    （1）求证：数列{an+n}为等比数列；
    （2）记bn=an+（1﹣λ）n，且数列{bn}的前n项和为Tn ， 若T3为数列{Tn}中的最小项，求λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知平面五边形是轴对称图形(如图1)，BC为对称轴，AD⊥CD，AD=AB=1，，将此五边形沿BC折叠，使平面ABCD⊥平面BCEF，得到如图2所示的空间图形，对此空间图形解答下列问题.

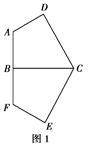
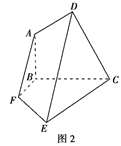
    （1）证明：AF∥平面DEC；

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】南航集团与波音公司2018年2月在广州签署协议，双方合作的客改货项目落户广州空港经济区．根据协议，双方将在维修技术转让、支持项目、管理培训等方面开展战略合作．现组织者对招募的100名服务志愿者培训后，组织一次知识竞赛，将所得成绩制成如下频率分布直方图（假定每个分数段内的成绩均匀分布），组织者计划对成绩前20名的参赛者进行奖励．

    （1）试求受奖励的分数线；

    （2）从受奖励的20人中利用分层抽样抽取5人，再从抽取的5人中抽取2人在主会场服务，试求2人成绩都在90分以上（含90分）的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥P－ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA＝AB＝BC＝2，D为线段AC的中点，E为线段PC上一点.

    (1)求证：PA⊥BD；

    (2)求证：平面BDE⊥平面PAC；

    (3)当PA∥平面BDE时，求三棱锥E－BCD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知平行四边形ABCD中．∠BAD=120°，AB=1，AD=2，点P是线段BC上的一个动点，则 的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】小明跟父母、爷爷奶奶一同参加《中国诗词大会》的现场录制，5人坐成一排.若小明的父母至少有一人与他相邻，则不同坐法的总数为

    A. 60 B. 72 C. 84 D. 96

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4﹣4：坐标系与参数方程 曲线C1的参数方程为 （α为参数），在以原点O为极点，x轴的正半轴为极轴的极坐标系中，曲线C2的极坐标方程为ρcos2θ=sinθ．
    （1）求曲线C1的极坐标方程和曲线C2的直角坐标方程；
    （2）若射线l：y=kx（x≥0）与曲线C1 ， C2的交点分别为A，B（A，B异于原点），当斜率k∈（1， ]时，求|OA||OB|的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥中，底面ABCD是矩形，平面ABCD，，E，F是线段BC，AB的中点．

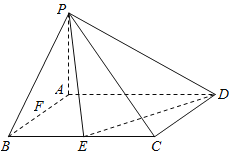
    Ⅰ证明：；

    Ⅱ在线段PA上确定点G，使得平面PED，请说明理由．

    查看答案和解析>>

    同步练习册答案