考点:三角函数的化简求值,余弦定理,三角函数的最值
专题:计算题,三角函数的求值
分析:(1)先利用三角变换公式将其化简得sin(A-
)=
,从而由角A的范围求得角A的值;
(2)先利用二倍角公式和同角三角函数基本关系式将已知三角函数式化为二次齐次式,再两边同除以cos
2B得关于tanB的方程,解得tanB的值,再利用两角和的正切公式计算所求值即可.
解答:
解:(1)∵A,B,C是△ABC的三内角,
sinA-cosA=1
∴可得:2sin(A-
)=1,即有:sin(A-
)=
∵0<A<π,可得-
<A
-<
∴可解得:A
-=
∴A=
.
(2)由
=-3⇒
=-3⇒1+sin2B=-3cos2B⇒sin2B+3cos2B=-1.
可得:2sinBcosB+3(cos
2B-sin
2B)=-(sin
2B+cos
2B)
两边同除以cos
2B得:2tanB+3(1-tan
2B)=-(tan
2B+1)
化简得tan
2B-tanB-2=0
∴tanB=-1或tanB=2
若tanB=-1,则B=
,此时A+B>π,不合题意;
若tanB=2,则tanC=-tan(A+B)=-
=-
=
.
点评:本题主要考查了向量数量积的运算性质,三角变换公式在三角化简即求值中的应用,二倍角公式及二次齐次式的解题技巧,属基础题.



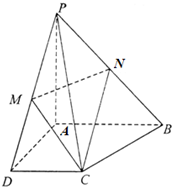 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,且PA=4,底面ABCD为梯形,
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,且PA=4,底面ABCD为梯形,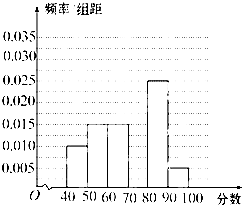 2012年3月10日某校组织同学听取了温家宝总理所作的政府工作报告,并进行了检测,从参加检测的高二学生中随机抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
2012年3月10日某校组织同学听取了温家宝总理所作的政府工作报告,并进行了检测,从参加检测的高二学生中随机抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: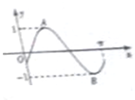 已知函数f(x)=2sinxcos(x-φ)-
已知函数f(x)=2sinxcos(x-φ)-