【题目】一场小型晚会有
个唱歌节目和
个相声节目，要求排出一个节目单．
（1）个相声节目要排在一起，有多少种排法？
（2）个相声节目彼此要隔开，有多少种排法？
（3）第一个节目和最后一个节目都是唱歌节目，有多少种排法？
（4）前个节目中要有相声节目，有多少种排法？
（要求：每小题都要有过程，且计算结果都用数字表示）
【答案】（1）
；（2）
；（3）
；（4）
.
【解析】
（1）将
个相声节目进行捆绑，与其它
个节目形成
个元素，利用捆绑法可求得排法种数；
（2）将个相声节目插入其它个节目所形成的空中，利用插空法可求得排法种数；
（3）第一个节目和最后一个节目都是唱歌节目，则个节目排在中间，利用分步乘法计数原理可求得排法种数；
（4）在
个节目进行全排的排法种数中减去前个节目中没有相声节目的排法种数，由此可求得结果.
（1）将个相声节目进行捆绑，与其它个节目形成个元素，然后进行全排，
所以，排法种数为
种；
（2）将个相声节目插入其它个节目所形成的个空中，则排法种数为
种；
（3）第一个节目和最后一个节目都是唱歌节目，则其它个节目排在中间，进行全排，
由分步乘法计数原理可知，排法种数为
种；
（4）在个节目进行全排的排法种数中减去前个节目中没有相声节目的排法种数，
可得出前个节目中要有相声节目的排法种数为
.
科目：高中数学 来源： 题型：
【题目】以下四个命题中，正确的题号是__________.
①函数的最值一定是极值；
②设
：实数
，
满足
；
：实数，满足
，则是的充分不必要条件；
③已知椭圆
：
与双曲线
：
的焦点重合，
、
分别为、的离心率，则
，且
；
④一动圆
过定点
，且与已知圆
：
相切，则动圆圆心的轨迹方程是
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】十九大提出，加快水污染防治，建设美丽中国.根据环保部门对某河流的每年污水排放量
（单位：吨）的历史统计数据，得到如下频率分布表：
将污水排放量落入各组的频率作为概率，并假设每年该河流的污水排放量相互独立.
（1）求在未来3年里，至多1年污水排放量
的概率；（2）该河流的污水排放对沿河的经济影响如下：当
时，没有影响；当
时，经济损失为10万元；当
时，经济损失为60万元.为减少损失，现有三种应对方案：
方案一：防治350吨的污水排放，每年需要防治费3.8万元；
方案二：防治310吨的污水排放，每年需要防治费2万元；
方案三：不采取措施.
试比较上述三种文案，哪种方案好，并请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆C的两个焦点分别为F1（-1，0）、F2（1，0），短轴的两个端点分别为B1，B2
（1）若△F1B1B2为等边三角形，求椭圆C的方程；
（2）若椭圆C的短轴长为2，过点F2的直线l与椭圆C相交于P，Q两点，且
，求直线l的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】随着共享单车的成功运营，更多的共享产品逐步走人大家的世界，共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷，某公司随机抽取1000人对共享产品是否对日常生活有益进行了问卷调查，并对参与调查的1000人中的性别以及意见进行了分类，得到的数据如下表所示：
男 | 女 | 总计 | |
认为共享产品对生活有益 |
|
|
|
认为共享产品对生活无益 |
|
|
|
总计 |
|
|
|
（1）求出表格中
的值，并根据表中的数据，判断能否在犯错误的概率不超过
的前提下，认为对共享产品的态度与性别有关系？
（2）现按照分层抽样从认为共享产品对生活无益的人员中随机抽取6人，再从6人中随机抽取2人赠送超市购物券作为答谢，求恰有1人是女性的概率.
参考公式：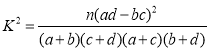
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程:
已知极坐标系的极点在直角坐标系的原点，极轴与x轴非负半轴重合，直线l的参数方程为：
（t为参数，a∈[0，π），曲线C的极坐标方程为：p＝2cosθ．
（Ⅰ）写出曲线C在直角坐标系下的标准方程；
（Ⅱ）设直线l与曲线C相交PQ两点，若|PQ|
，求直线l的斜率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
