
【题目】△ABC中,角A,B,C的对边分别是a,b,c且满足(2a﹣c)cosB=bcosC.
(1)求角B的大小;
(2)若△ABC的面积为 ![]() ,求a+c的值.
,求a+c的值.
【答案】
(1)解:又A+B+C=π,即C+B=π﹣A,
∴sin(C+B)=sin(π﹣A)=sinA,
将(2a﹣c)cosB=bcosC,利用正弦定理化简得:(2sinA﹣sinC)cosB=sinBcosC,
∴2sinAcosB=sinCcosB+sinBcosC=sin(C+B)=sinA,
在△ABC中,0<A<π,sinA>0,
∴cosB= ![]() ,又0<B<π,
,又0<B<π,
则B= ![]()
(2)解:∵△ABC的面积为 ![]() ,sinB=sin
,sinB=sin ![]() =
= ![]() ,
,
∴S= ![]() acsinB=
acsinB= ![]() ac=
ac= ![]() ,
,
∴ac=6,又b= ![]() ,cosB=cos
,cosB=cos ![]() =
= ![]() ,
,
∴利用余弦定理b2=a2+c2﹣2accosB得:a2+c2﹣ac=(a+c)2﹣3ac=(a+c)2﹣18=3,
∴(a+c)2=21,
则a+c= ![]()
【解析】(1)利用正弦定理化简已知的等式,整理后利用两角和与差的正弦函数公式及诱导公式化简,根据sinA不为0,得到cosB的值,利用特殊角的三角函数值即可求出B的度数;(2)由B的度数求出sinB和cosB的值,利用三角形的面积公式表示出三角形ABC的面积,将sinB及已知的面积代入求出ac的值,利用余弦定理得到b2=a2+c2﹣2accosB,再利用完全平方公式整理后,将b,ac及cosB的值代入,开方即可求出a+c的值.
【考点精析】掌握正弦定理的定义和余弦定理的定义是解答本题的根本,需要知道正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数列{an}的前 n 项和为 Sn , a1=1,且 an+1=2Sn+1,n∈N .
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令 c=log3a2n , bn= ![]() ,记数列{bn}的前 n 项和为Tn , 若对任意 n∈N , λ<Tn 恒成立,求实数 λ 的取值范围.
,记数列{bn}的前 n 项和为Tn , 若对任意 n∈N , λ<Tn 恒成立,求实数 λ 的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a、b、c是角A、B、C的对边,则下列结论正确的序号是 . ①若a、b、c成等差数列,则B= ![]() ; ②若c=4,b=2
; ②若c=4,b=2 ![]() ,B=
,B= ![]() ,则△ABC有两解;
,则△ABC有两解;
③若B= ![]() ,b=1,ac=2
,b=1,ac=2 ![]() ,则a+c=2+
,则a+c=2+ ![]() ; ④若(2c﹣b)cosA=acosB,则A=
; ④若(2c﹣b)cosA=acosB,则A= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若集合M满足:x,y∈M,都有x+y∈M,xy∈M,则称集合M是封闭的.显然,整数集Z,有理数集Q都是封闭的.对于封闭的集合M(MR),f:M→M是从集合到集合的一个函数, ①如果都有f(x+y)=f(x)+f(y),就称是保加法的;
②如果x,y∈M都有f(xy)=f(x)f(y),就称f是保乘法的;
③如果f既是保加法的,又是保乘法的,就称f在M上是保运算的.
在上述定义下,集合 ![]() 封闭的(填“是”或“否”);若函数f(x)在Q上保运算,并且是不恒为零的函数,请写出满足条件的一个函数f(x)= .
封闭的(填“是”或“否”);若函数f(x)在Q上保运算,并且是不恒为零的函数,请写出满足条件的一个函数f(x)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期是π,若其图象向右平移
)的最小正周期是π,若其图象向右平移 ![]() 个单位后得到的函数为奇函数,则函数y=f(x)的图象( )
个单位后得到的函数为奇函数,则函数y=f(x)的图象( )
A.关于点( ![]() ,0)对称?
,0)对称?
B.关于直线x= ![]() 对称
对称
C.关于点( ![]() ,0)对称?
,0)对称?
D.关于直线x= ![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (其中α为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ. (Ⅰ)若A,B为曲线C1 , C2的公共点,求直线AB的斜率;
(其中α为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ. (Ⅰ)若A,B为曲线C1 , C2的公共点,求直线AB的斜率;
(Ⅱ)若A,B分别为曲线C1 , C2上的动点,当|AB|取最大值时,求△AOB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC中,PC⊥平面ABC,PC=3,∠ACB= ![]() .D,E分别为线段AB,BC上的点,且CD=DE=
.D,E分别为线段AB,BC上的点,且CD=DE= ![]() ,CE=2EB=2.
,CE=2EB=2.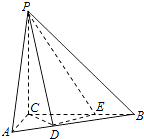
(Ⅰ)证明:DE⊥平面PCD
(Ⅱ)求二面角A﹣PD﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的长轴长为4,离心率为
=1(a>b>0)的长轴长为4,离心率为 ![]() ,右焦点为F.
,右焦点为F.
(1)求椭圆C的方程;
(2)直线l与椭圆C相切于点P(不为椭圆C的左、右顶点),直线l与直线x=2交于点A,直线l与直线x=﹣2交于点B,请问∠AFB是否为定值?若不是,请说明理由;若是,请证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com