
【题目】解关于x的不等式:(ax﹣1)(x﹣1)>0.
【答案】解:因为关于x的不等式:(ax﹣1)(x﹣1)>0, 所以当a=0时,即(﹣1)(x﹣1)>0,
此时解集为(﹣∞,1);
当a≠0时,即a(x﹣1)(x﹣ ![]() )>0;
)>0;
①a<0时即(x﹣1)(x﹣ ![]() )<0,其中
)<0,其中 ![]() <0<1,
<0<1,
此时不等式的解集为( ![]() ,1);
,1);
②0<a<1时即(x﹣1)(x﹣ ![]() )>0,其中
)>0,其中 ![]() >1,
>1,
此时不等式的解集为(﹣∞,1)∪( ![]() ,+∞);
,+∞);
③a=1时即(x﹣1)2>0,
此时不等式的解集为{x|x∈R且x≠1};
④a>1时即(x﹣1)(x﹣ ![]() )>0,其中
)>0,其中 ![]() <1,
<1,
此时不等式的解集为(﹣∞, ![]() )∪(1,+∞)
)∪(1,+∞)
【解析】讨论a=0、a≠0时,再分a<0、0<a<1和a=1、a>1时,求出对应不等式的解集.
【考点精析】掌握解一元二次不等式是解答本题的根本,需要知道求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】直线l过P(1,2),且A(2,3),B(4,﹣5)到l的距离相等,则直线l的方程是( )
A.4x+y﹣6=0
B.x+4y﹣6=0
C.3x+2y﹣7=0或4x+y﹣6=0
D.2x+3y﹣7=0或x+4y﹣6=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,PA⊥底面ABCD,AB⊥AC,AB=1,BC=2,PA= ![]() ,E为BC的中点.
,E为BC的中点. 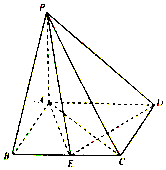
(1)证明:PE⊥ED;
(2)求二面角E﹣PD﹣A的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() .
.
(1)求函数![]() 的单调增区间;
的单调增区间;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数![]() 的图象,若
的图象,若![]() 在
在![]() 上至少含有10个零点,求
上至少含有10个零点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若在曲线f(x,y)=0(或y=f(x))上两个不同点处的切线重合,则称这条切线为曲线f(x,y)=0或y=f(x)的“自公切线”.下列方程:
①x2﹣y2=1;
②y=x2﹣|x|;
③y=3sinx+4cosx;
④|x|+1= ![]()
对应的曲线中存在“自公切线”的有( )
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值;
的距离的最大值;
(2)若曲线![]() 上的所有点都在直线
上的所有点都在直线![]() 的下方,求实数
的下方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cos2ωx+2sinωxcosωx(ω>0)的最小正周期为π.
(1)求f( ![]() )的值;
)的值;
(2)求函数f(x)的单调递增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com