
【题目】如图,梯形ABCD内接于⊙O,AD∥BC,过点C作⊙O的切线,交BD的延长线于点P,交AD的延长线于点E. 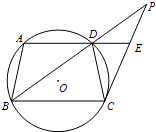
(1)求证:AB2=DEBC;
(2)若BD=9,AB=6,BC=9,求切线PC的长.
【答案】
(1)解:∵AD∥BC
∴AB=DC,∠EDC=∠BCD,
又PC与⊙O相切,∴∠ECD=∠DBC,
∴△CDE∽△BCD,∴ ![]() ,
,
∴CD2=DEBC,即AB2=DEBC
(2)解:由(1)知, ![]() ,
,
∵△PDE∽△PBC,
∴ ![]() .
.
又∵PB﹣PD=9,
∴ ![]() .
.
∴ ![]() .
.
∴ ![]()
【解析】对于(1)求证:AB2=DEBC,根据题目可以判断出梯形为等腰梯形,故AB=CD,然后根据角的相等证△CDE相似于△BCD,根据相似的性质即可得到答案.
对于(2)由BD=9,AB=6,BC=9,求切线PC的长.根据弦切公式可得PC2=PDPB,然后根据相似三角形边成比例的性质求出PD和PB代入即可求得答案.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+φ),其中φ为实数,若f(x)≤|f( ![]() )|对x∈R恒成立,且f(
)|对x∈R恒成立,且f( ![]() )>f(π),则f(x)的单调递增区间是( )
)>f(π),则f(x)的单调递增区间是( )
A.[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
B.[kπ,kπ+ ![]() ](k∈Z)
](k∈Z)
C.[kπ+ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
D.[kπ﹣ ![]() ,kπ](k∈Z)
,kπ](k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几个孩子在一棵枯树上玩耍,他们均不慎失足下落.已知
(![]() )甲在下落的过程中依次撞击到树枝
)甲在下落的过程中依次撞击到树枝![]() ,
,![]() ,
,![]() ;
;
(![]() )乙在下落的过程中依次撞击到树枝
)乙在下落的过程中依次撞击到树枝![]() ,
,![]() ,
,![]() ;
;
(![]() )丙在下落的过程中依次撞击到树枝
)丙在下落的过程中依次撞击到树枝![]() ,
,![]() ,
,![]() ;
;
(![]() )丁在下落的过程中依次撞击到树枝
)丁在下落的过程中依次撞击到树枝![]() ,
,![]() ,
,![]() ;
;
(![]() )戊在下落的过程中依次撞击到树枝
)戊在下落的过程中依次撞击到树枝![]() ,
,![]() ,
,![]() .
.
倒霉和李华在下落的过程中撞到了从![]() 到
到![]() 的所有树枝,根据以上信息,在李华下落的过程中,和这
的所有树枝,根据以上信息,在李华下落的过程中,和这![]() 根树枝不同的撞击次序有( )种.
根树枝不同的撞击次序有( )种.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2018年高校自主招生期间,某校把学生的平时成绩按“百分制”折算,选出前![]() 名学生,并对这
名学生,并对这![]() 名学生按成绩分组,第一组
名学生按成绩分组,第一组![]() ,第二组
,第二组![]() ,第三组
,第三组![]() ,第四组
,第四组![]() ,第五组
,第五组![]() .如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为60.
.如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为60.

(1)请写出第一、二、三、五组的人数,并在图中补全频率分布直方图;
(2)若![]() 大学决定在成绩高的第3,4,5组中用分层抽样的方法抽取6名学生进行面试.
大学决定在成绩高的第3,4,5组中用分层抽样的方法抽取6名学生进行面试.
①若![]() 大学本次面试中有
大学本次面试中有![]() ,
,![]() ,
,![]() 三位考官,规定获得至少两位考官的认可即为面试成功,且各考官面试结果相互独立.已知甲同学已经被抽中,并且通过这三位考官面试的概率依次为
三位考官,规定获得至少两位考官的认可即为面试成功,且各考官面试结果相互独立.已知甲同学已经被抽中,并且通过这三位考官面试的概率依次为![]() ,
,![]() ,
,![]() ,求甲同学面试成功的概率;
,求甲同学面试成功的概率;
②若![]() 大学决定在这6名学生中随机抽取3名学生接受考官
大学决定在这6名学生中随机抽取3名学生接受考官![]() 的面试,第3组有
的面试,第3组有![]() 名学生被考官
名学生被考官![]() 面试,求
面试,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂对一批新产品的长度(单位:![]() )进行检测,如下图是检测结果的频率分布直方图,据此估计这批产品的中位数与平均数分别为( )
)进行检测,如下图是检测结果的频率分布直方图,据此估计这批产品的中位数与平均数分别为( )

A.20,22.5B.22.5,25C.22.5,22.75D.22.75,22.75
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com