
分析 (1)已知函数f(x)=x3+3ax2+bx+a2在x=1处有极值0,即f(-1)=0,f′(-1)=0,通过求导函数,再代入列方程组,即可解得a、b的值;
(2)分别解不等式f′(x)>0和f′(x)<0,即可得函数f(x)的单调增区间与单调递减区间.
(3)利用(1)(2)的结果直接求解函数的极值即可.
解答 解:(1)∵f′(x)=3x2+6ax+b,(a>1)函数f(x)=x3+3ax2+bx+a2在x=-1处有极值0,
∴f(-1)=0,f′(-1)=0
∴-1+3a-b+a2=0,3-6a+b=0.
解得a=2,b=9.
(2)f(x)=x3+6x2+9x+4,
∴f′(x)=3x2+12x+9
∴由f′(x)=3x2+12x+9>0得x∈(-∞,-3)或(-1,+∞)
由f′(x)=3x2+12x+9<0得x∈(-3,-1)
∴函数f(x)的单调增区间为:(-∞,-3),(-1,+∞),减区间为:(-3,-1).
(3)由(2)可知f(x)的极小值:f(-1)=0,
极大值为:f(-3)=-27+54-27+4=4.
点评 本题考查导数在求函数极值中的应用,利用导数求函数的单调区间,属于中档题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:解答题
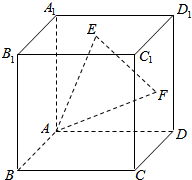 如图,在正方体ABCD-A1B1C1D1中,E、F分别为A1B1C1D1,CDD1C1的中心,试用向量$\overrightarrow{{B}_{1}B}$,$\overrightarrow{{B}_{1}{C}_{1}}$,$\overrightarrow{{B}_{1}{A}_{1}}$表示向量:
如图,在正方体ABCD-A1B1C1D1中,E、F分别为A1B1C1D1,CDD1C1的中心,试用向量$\overrightarrow{{B}_{1}B}$,$\overrightarrow{{B}_{1}{C}_{1}}$,$\overrightarrow{{B}_{1}{A}_{1}}$表示向量:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{21-6\sqrt{3}}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
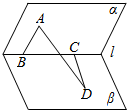 如图,已知B、C是二面角α-l-β棱上两点AB?α,AB⊥l,CD?β,CD⊥l,AB=BC=1,CD=$\sqrt{3}$,AD=2$\sqrt{2}$,则二面角α-l-β的大小是150°.
如图,已知B、C是二面角α-l-β棱上两点AB?α,AB⊥l,CD?β,CD⊥l,AB=BC=1,CD=$\sqrt{3}$,AD=2$\sqrt{2}$,则二面角α-l-β的大小是150°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com