练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知等比数列{an}的前三项依次为a﹣2，a+2，a+8，则an=（ ）
    A.
    B.
    C.
    D.

    【答案】C
    【解析】解：∵a﹣2，a+2，a+8为等比数列{an}的前三项，
    ∴（a+2）2=（a﹣2）（a+8），即a2+4a+4=a2+6a﹣16，
    解得：a=10，
    ∴等比数列{an}的前三项依次为8，12，18，
    即等比数列的首项为8，公比为 = ，
    则此等比数列的通项公式an= ．
    故选C
    【考点精析】根据题目的已知条件，利用等比数列的通项公式（及其变式）和等比数列的基本性质的相关知识可以得到问题的答案，需要掌握通项公式：；{an}为等比数列，则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，直角三角形ABC的顶点坐标A（﹣2，0），直角顶点B（0，﹣2 ），顶点C在x轴上，点P为线段OA的中点，三角形ABC外接圆的圆心为M．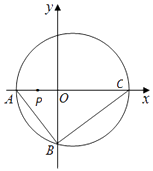

    （1）求BC边所在直线方程；
    （2）求圆M的方程；
    （3）直线l过点P且倾斜角为 ，求该直线被圆M截得的弦长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两名同学在五次考试中数学成绩统计用茎叶图如表示如图2所示，则甲的平均成绩比乙的平均成绩（填高、低、相等）；甲成绩的方差比乙成绩的方差（填大、小）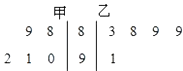

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆O的方程为x2+y2=5．
    （1）P是直线y= x﹣5上的动点，过P作圆O的两条切线PC、PD，切点为C、D，求证：直线CD过定点；
    （2）若EF、GH为圆O的两条互相垂直的弦，垂足为M（1，1），求四边形EGFH面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知{an}是等差数列，Sn是其前n项和，
    （1）a2=﹣1，S15=75，求an与Sn；
    （2）a1+a2+a3+a4=124，an+an﹣1+an﹣2+an﹣3=156，Sn=210，求项数n．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】{an}满足a1=4，且an=4﹣ （n＞1），记bn= ．
    （1）求证：{bn}为等差数列．
    （2）求{an}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a，b，c分别为△ABC三个内角A，B，C所对的边长，且acosB﹣bcosA= c．
    （1）求 的值；
    （2）若A=60°，求 的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义：若函数f（x）对于其定义域内的某一数x0 ， 有 f（x0）=x0 ， 则称x0是f （x）的一个不动点．已知函数f（x）=ax2+（b+1）x+b﹣1 （a≠0）．
    （1）当a=1，b=﹣2时，求函数f（x）的不动点；
    （2）若对任意的实数b，函数f（x）恒有两个不动点，求a的取值范围；
    （3）在（2）的条件下，若y=f（x）图象上两个点A，B的横坐标是函数f（x）的不动点，且A，B两点关于直线y=kx+ 对称，求b的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正方形BCDE的边长为a，已知AB= BC，将△ABE沿边BE折起，折起后A点在平面BCDE上的射影为D点，则翻折后的几何体中有如下描述：
    ① AB与DE所成角的正切值是 ；
    ②AB∥CE
    ③VB﹣ACE体积是 a3；
    ④平面ABC⊥平面ADC．
    其中正确的有 ． （填写你认为正确的序号）

    查看答案和解析>>

    同步练习册答案