
【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50m/min.在甲出发2min后,乙从A乘缆车到B,在B处停留1min后,再从B匀速步行到C.假设缆车匀速直线运动的速度为130m/min,山路AC长为1260m,经测量,cosA= ![]() ,cosC=
,cosC= ![]()
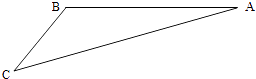
(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(3)为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
【答案】
(1)解:在△ABC中,因为cosA= ![]() ,cosC=
,cosC= ![]() ,所以sinA=
,所以sinA= ![]() ,sinC=
,sinC= ![]() ,
,
从而sinB=sin[π﹣(A+C)]=sin(A+C)=sinAcosC+cosAsinC= ![]() =
= ![]()
由正弦定理 ![]() ,得AB=
,得AB= ![]() =
= ![]() =1040m.
=1040m.
所以索道AB的长为1040m.
(2)解:假设乙出发t分钟后,甲、乙两游客距离为d,此时,甲行走了(100+50t)m,乙距离A处130t m,所以由余弦定理得
d2=(100+50t)2+(130t)2﹣2×130t×(100+50t)× ![]() =200(37t2﹣70t+50)=200[37(t﹣
=200(37t2﹣70t+50)=200[37(t﹣ ![]() )2+
)2+ ![]() ],
],
因0≤t≤ ![]() ,即0≤t≤8,故当t=
,即0≤t≤8,故当t= ![]() min时,甲、乙两游客距离最短
min时,甲、乙两游客距离最短
(3)解:由正弦定理 ![]() ,得BC=
,得BC= ![]() =
= ![]() =500m,
=500m,
乙从B出发时,甲已经走了50×(2+8+1)=550m,还需走710m才能到达C.
设乙步行的速度为 v m/min,由题意得﹣3≤ ![]() ≤3,解得
≤3,解得 ![]() ,所以为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在[
,所以为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在[ ![]() ]范围内
]范围内
【解析】(1)根据正弦定理即可确定出AB的长;(2)设乙出发t分钟后,甲、乙两游客距离为d,此时,甲行走了(100+50t)m,乙距离A处130t m,由余弦定理可得;(3)设乙步行的速度为 v m/min,从而求出v的取值范围.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在棱台![]() 中,
中, ![]() 与
与![]() 分别是棱长为1与2的正三角形,平面
分别是棱长为1与2的正三角形,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点,
中点, ![]() (
(![]() ,
, ![]() ).
).

(1)设![]() 中点为
中点为![]() ,
, ![]() ,求证:
,求证: ![]() 平面
平面![]() ;
;
(2)若![]() 到平面
到平面![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点P(﹣3,﹣4)作直线l,当l的斜率为何值时
(1)l将圆(x﹣1)2+(y+2)2=4平分?
(2)l与圆(x﹣1)2+(y+2)2=4相切?
(3)l与圆(x﹣1)2+(y+2)2=4相交且所截得弦长=2?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两条直线l1(3+m)x+4y=5﹣3m,l2 2x+(5+m)y=8.当m分别为何值时,l1与l2:
(1)相交?
(2)平行?
(3)垂直?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,已知cosA= ![]() ,b=5c.
,b=5c.
(1)求sinC;
(2)若△ABC的面积S= ![]() sinBsinC,求a的值.
sinBsinC,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某大学自主招生的面试中,考生要从规定的6道科学题,4道人文题共10道题中,随机抽取3道作答,每道题答对得10分,答错或不答扣5分,已知甲、乙两名考生参加面试,甲只能答对其中的6道科学题,乙答对每道题的概率都是![]() ,每个人答题正确与否互不影响.
,每个人答题正确与否互不影响.
(1)求考生甲得分![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(2)求甲,乙两人中至少有一人得分不少于15分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一周期内的图象时,列表并填入了部分数据,如下表:
)在某一周期内的图象时,列表并填入了部分数据,如下表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 3 | 0 |
(1)请将上表空格中的数据在答卷的相应位置上,并求函数f(x)的解析式;
(2)若y=f(x)的图象上所有点向左平移 ![]() 个单位后对应的函数为g(x),求当x∈[﹣
个单位后对应的函数为g(x),求当x∈[﹣ ![]() ,
, ![]() ]时,函数y=g(x)的值域.
]时,函数y=g(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从参加某次高中英语竞赛的学生中抽出100名,将其成绩整理后,绘制频率分布直方图(如图所示).其中样本数据分组区间为: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
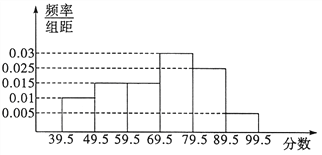
(Ⅰ)试求图中![]() 的值,并计算区间
的值,并计算区间![]() 上的样本数据的频率和频数;
上的样本数据的频率和频数;
(Ⅱ)试估计这次英语竞赛成绩的众数、中位数及平均成绩(结果精确到![]() ).
).
注:同一组数据用该组区间的中点值作为代表
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com