
已知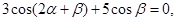 则
则 的值为( )
的值为( )
A 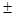 4 B 4 C -4 D 1
4 B 4 C -4 D 1
C
解析考点:三角函数恒等式的证明.
分析:利用配角法,将2α+β化成(α+β)+α,的形式,β化成(α+β)-α,的形式,再结合三角函数的和角公式化简即可.
解:3cos[(α+β)+α]+5cosβ=得,
即3cos(α+β)?cosα-3sin(α+β)?sinα+5cosβ=得.
3cos(α+β)cosα-3sin(α+β)sinα+5cos[(α+β)-α]=得,
3cos(α+β)cosα-3sin(α+β)?sinα+5cos(α+β)?cosα+5sin(α+β)?sinα=得,
8cos(α+β)?cosα+2sin(α+β)?sinα=得,
8+2tan(α+β)?tanα=得,
∴tan(α+β)tanα=-4.
答案:-4.
点评:本题主要考查知识点是三角函数的化简、求值及恒等式的证明、配角法.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com