
【题目】在等差数列{an}中,a1 =-2,a12 =20.
(1)求数列{an}的通项an ;
(2)若bn=![]() ,求数列{
,求数列{![]() }的前n项和.
}的前n项和.
科目:高中数学 来源: 题型:
【题目】有下列命题:
①在函数![]() 的图象中,相邻两个对称中心的距离为
的图象中,相邻两个对称中心的距离为![]() ;②函数
;②函数![]() 的图象关于点
的图象关于点![]() 对称;③“
对称;③“ ![]() 且
且![]() ”是“
”是“![]() ”的必要不充分条件;④已知命题
”的必要不充分条件;④已知命题![]() :对任意的
:对任意的![]() ,都有
,都有![]() ,则
,则![]() 是:存在
是:存在![]() ,使得
,使得![]() ;⑤在
;⑤在![]() 中,若
中,若![]() ,
, ![]() ,则角
,则角![]() 等于
等于![]() 或
或![]() .其中所有真命题的个数是__________.
.其中所有真命题的个数是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(Ⅰ)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设曲线![]() 经过伸缩变换
经过伸缩变换 得到曲线
得到曲线![]() ,若点
,若点![]() ,直线
,直线![]() 与
与![]() 交与
交与![]() ,
, ![]() ,求
,求![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一人答一份).现从回收的年龄在2060岁的问卷中随机抽取了100份, 统计结果如下面的图表所示.
年龄 分组 | 抽取份 数 | 答对全卷的人数 | 答对全卷的人数占本组的概率 |
[20,30) | 40 | 28 | 0.7 |
[30,40) | n | 27 | 0.9 |
[40,50) | 10 | 4 | b |
[50,60] | 20 | a | 0.1 |
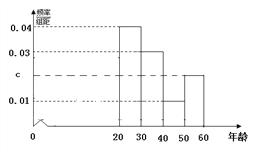
(1)分别求出n, a, b, c的值;
(2)从年龄在[40,60]答对全卷的人中随机抽取2人授予“环保之星”,求年龄在[50,60] 的人中至少有1人被授予“环保之星”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】运货卡车以每小时x千米的速度匀速行驶130千米(50≤x≤100)(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油(2+ ![]() )升,司机的工资是每小时14元.
)升,司机的工资是每小时14元.
(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
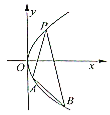
【题目】【广西名校2017届高三上学期第一次摸底】如图,过抛物线![]() 上一点
上一点![]() ,作两条直线分别交抛物线于
,作两条直线分别交抛物线于![]() ,
,![]() ,
,
当![]() 与
与![]() 的斜率存在且倾斜角互补时:
的斜率存在且倾斜角互补时:
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若直线![]() 在
在![]() 轴上的截距
轴上的截距![]() 时,求
时,求![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com