(选修4-5:不等式选讲)已知函数f(x)=|x+3|+|x-a|(a>0).
(Ⅰ)当a=4时,已知f(x)=7,求x的取值范围;
(Ⅱ)若f(x)≥6的解集为{x|x≤-4或x≥2},求a的值.
【答案】
分析:(I)当a=4时,根据绝对值的性质,我们求出当(x+3)(4-x)≥0时,即-3≤x≤4时f(x)=|x+3|+|x-4|取最小值7.
(II)根据不等式的根与对应方程根的关系,可得-4和2是方程f(x)=|x+3|+|x-a|=0的两根,解方程组可得a的值
解答:解:(I)当a=4时,函数f(x)=|x+3|+|x-4|=|x+3|+|4-x|≥|x+3+4-x|=7
当且仅当(x+3)(4-x)≥0时,即-3≤x≤4时取等号
故x的取值范围为[-3,4]
(II)若f(x)≥6的解集为{x|x≤-4或x≥2},
则-4和2是方程f(x)=|x+3|+|x-a|=0的两根
即
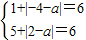
解得a=1
点评:本题考查的知识点是带绝对值的函数,熟练掌握绝对值的性质及不等式解集的端点与对应方程根之间的关系是解答的关键.

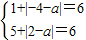


 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,