
 •
• =3,a=2
=3,a=2 ,b+c=6,求cosA.
,b+c=6,求cosA. x+sin(
x+sin( x-
x- )+1,y=g(x)与y=f(x)的图象关于直线x=1对称,当x∈[-
)+1,y=g(x)与y=f(x)的图象关于直线x=1对称,当x∈[- ,0]时,求y=g(x)的最大值.
,0]时,求y=g(x)的最大值. •
• =3,∴bc•cosA=3. (1分)
=3,∴bc•cosA=3. (1分) =62-2bc-2×3,∴bc=5,(5分)
=62-2bc-2×3,∴bc=5,(5分) . (6分)
. (6分) x+sin(
x+sin( x-
x- )+1=sin
)+1=sin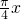 cos
cos -cos
-cos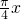 sin
sin -cos
-cos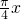 =
= sin
sin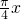 -
- cos
cos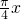 =
= sin(
sin(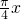 -
- ).(8分)
).(8分) sin[
sin[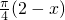 -
- ]=
]= cos(
cos(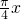 +
+ ). (10分)
). (10分) ,0],∴
,0],∴ ≤(
≤(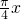 +
+ )≤
)≤ ,
, cos(
cos(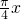 +
+ )的最大值为
)的最大值为  ×
× =
= ,即 当x∈[-
,即 当x∈[- ,0]时,求y=g(x)的最大值为
,0]时,求y=g(x)的最大值为  .(12分)
.(12分) •
• =3,可得 bc•cosA=3,再由余弦定理求得 bc=5,由此求得 cosA=
=3,可得 bc•cosA=3,再由余弦定理求得 bc=5,由此求得 cosA= .
.  sin(
sin(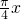 -
- ),根据对称性可得 g(x)=f(2-x)=
),根据对称性可得 g(x)=f(2-x)= cos(
cos(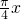 +
+ ),再由x∈[-
),再由x∈[- ,0],求得
,0],求得 cos(
cos(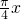 +
+ )的最大值,
)的最大值,

科目:高中数学 来源: 题型:
| ||
|
查看答案和解析>>
科目:高中数学 来源: 题型:
15
| ||
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| AB |
| AC |
| 5 |
| π |
| 8 |
| π |
| 4 |
| π |
| 6 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| AB |
| AC |
| 5 |
| π |
| 8 |
| π |
| 4 |
| π |
| 6 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
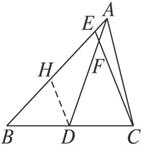
图1-20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com