
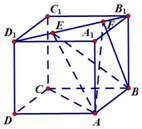
 如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且$EF=\frac{{\sqrt{2}}}{2}$,则下列结论中正确的是①②③④.
如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且$EF=\frac{{\sqrt{2}}}{2}$,则下列结论中正确的是①②③④.分析 ①,由EF∥平面ABCD判定;
②,动点E、F运动过程中,AC始终垂直面BEF;
③,三棱锥E-ABF的底△BEF的面积为定值,A到面BEF的距离为定值,故其体积为定值,;
④,令上底面中心为O,当E与D1重合时,此时点F与O重合,则两异面直线所成的角是∠OBC1,可求解∠OBC1=300.
解答  解:如图:
解:如图:
对于①,∵面ABCD∥面A1B1C1D1,EF?面A1B1C1D1,∴EF∥平面ABCD,故正确;
对于②,动点E、F运动过程中,AC始终垂直面BEF,∴平面ACF⊥平面BEF,故正确;
对于③,三棱锥E-ABF的底△BEF的面积为定值,A到面BEF的距离为定值,故其体积为定值,故正确;
对于④,令上底面中心为O,当E与D1重合时,此时点F与O重合,则两异面直线所成的角是∠OBC1,可求解∠OBC1=300,故正确.
故答案为:①②③④
点评 本题考查了空间线面、线线、面面位置关系,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 截距相等的直线都可以用方程$\frac{x}{a}+\frac{y}{a}=1$表示 | |
| B. | 方程x+my-2=0(m∈R)不能表示平行y轴的直线 | |
| C. | 经过点P(1,1),倾斜角为θ的直线方程为y-1=tanθ(x-1) | |
| D. | 经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线方程为$y-{y_1}=\frac{{{y_2}-{y_1}}}{{{x_2}-{x_1}}}(x-{x_1})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是一几何体的平面展开图,其中四边形ABCD为正方形,△PDC,△PBC,△PAB,△PDA为全等的等边三角形,E、F分别为PA、PD的中点,在此几何体中,下列结论中错误的为( )
如图是一几何体的平面展开图,其中四边形ABCD为正方形,△PDC,△PBC,△PAB,△PDA为全等的等边三角形,E、F分别为PA、PD的中点,在此几何体中,下列结论中错误的为( )| A. | 直线BE与直线CF共面 | B. | 直线BE与直线AF是异面直线 | ||
| C. | 平面BCE⊥平面PAD | D. | 面PAD与面PBC的交线与BC平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-∞,1) | C. | (-∞,-1) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {4,8} | B. | {0,2,4,10} | C. | {0,2,10} | D. | {0,2,6,10} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com