
分析 (1))△ABC中,由acosB=($\sqrt{2}$c-b)cosA,利用正弦定理求得cosA=$\frac{\sqrt{2}}{2}$,可得A的值.
(2)△ABC中,先由正弦定理求得AC的值,再由余弦定理求得AB的值,△ABD中,由余弦定理求得BD的值.
解答 解:(1)△ABC中,由acosB=($\sqrt{2}$c-b)cosA,利用正弦定理可得sinAcosB=$\sqrt{2}$sinCcosA-sinBcosA,
化简可得 sin(A+B)=$\sqrt{2}$sinCcosA,即 sinC=$\sqrt{2}$sinCcosA,求得cosA=$\frac{\sqrt{2}}{2}$,
∴A=$\frac{π}{4}$.
(2)由cosB=$\frac{2\sqrt{5}}{5}$,可得sinB=$\frac{\sqrt{5}}{5}$,再由正弦定理可得$\frac{a}{sinA}=\frac{b}{sinB}$,即$\frac{\sqrt{10}}{\frac{\sqrt{2}}{2}}=\frac{b}{\frac{\sqrt{5}}{5}}$,求得b=AC=2.
△ABC中,由余弦定理可得BC2=AB2+AC2-2AB•AC•cos∠A,即10=AB2+4-2AB•2•$\frac{\sqrt{2}}{2}$,求得AB=3$\sqrt{2}$.
△ABD中,由余弦定理可得 BD2=AB2+AD2-2AB•AD•cos∠A=18+1-6$\sqrt{2}$•$\frac{\sqrt{2}}{2}$=13,
∴BD=$\sqrt{13}$.
点评 本题主要考查正弦定理和余弦定理的应用,属于基本知识的考查.


科目:高中数学 来源: 题型:选择题
| A. | 等边三角形 | B. | 不含60°的等腰三角形 | ||
| C. | 钝角三角形 | D. | 直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
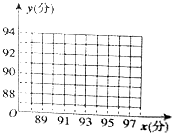 一次考试中,五名学生的数学、物理成绩如下表所示:
一次考试中,五名学生的数学、物理成绩如下表所示:| 学生 | A1 | A2 | A3 | A4 | A5 |
| 数学 | 89 | 91 | 93 | 95 | 97 |
| 物理 | 87 | 89 | 89 | 92 | 93 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com