
【题目】某企业生产A、B两种产品,生产每一吨产品所需的劳动力和煤、电耗如下表:
产品品种 | 劳动力 | 煤 | 电 |
A产品 | 3 | 9 | 4 |
B产品 | 10 | 4 | 5 |
已知生产每吨A产品的利润是7万元,生产每吨B产品的利润是12万元,现在条件有限,该企业仅有劳动力300个,煤360吨,并且供电局只能供电200千瓦,试问:该企业生产A、B两种产品各多少吨,才能获得最大利润?并求出最大利润.
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() 关于直线
关于直线![]() 对称且过点
对称且过点![]() 和
和![]() ,直线
,直线![]() 过定点
过定点![]() .
.
(1)证明:直线![]() 与圆
与圆![]() 相交;
相交;
(2)记直线![]() 与圆
与圆![]() 的两个交点为
的两个交点为![]() ,
,![]() .
.
①若弦长![]() ,求直线方程;
,求直线方程;
②求![]() 面积的最大值及
面积的最大值及![]() 面积的最大时的直线方程.
面积的最大时的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P和非零实数![]() ,若两条不同的直线
,若两条不同的直线![]() 均过点P,且斜率之积为
均过点P,且斜率之积为![]() ,则称直线
,则称直线![]() 是一组“
是一组“![]() 共轭线对”,如直
共轭线对”,如直![]() 是一组“
是一组“![]() 共轭线对”,其中O是坐标原点.
共轭线对”,其中O是坐标原点.
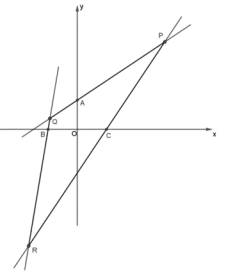
(1)已知![]() 是一组“
是一组“![]() 共轭线对”,求
共轭线对”,求![]() 的夹角的最小值;
的夹角的最小值;
(2)已知点A(0,1)、点![]() 和点C(1,0)分别是三条直线PQ,QR,RP上的点(A,B,C与P,Q,R均不重合),且直线PR,PQ是“
和点C(1,0)分别是三条直线PQ,QR,RP上的点(A,B,C与P,Q,R均不重合),且直线PR,PQ是“![]() 共轭线对”,直线QP,QR是“
共轭线对”,直线QP,QR是“![]() 共轭线对”,直线RP,RQ是“
共轭线对”,直线RP,RQ是“![]() 共轭线对”,求点P的坐标;
共轭线对”,求点P的坐标;
(3)已知点![]() ,直线
,直线![]() 是“
是“![]() 共轭线对”,当
共轭线对”,当![]() 的斜率变化时,求原点O到直线
的斜率变化时,求原点O到直线![]() 的距离之积的取值范围.
的距离之积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】边长为1的正方形![]() (及其内部)绕的
(及其内部)绕的![]() 旋转一周形成圆柱,如图,
旋转一周形成圆柱,如图,![]() 长为
长为![]() ,
,![]() 长为
长为![]() ,其中
,其中![]() 与
与![]() 在平面
在平面![]() 的同侧.
的同侧.
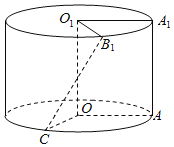
(1)求二面角![]() 的大小;(结果用反三角函数值表示)
的大小;(结果用反三角函数值表示)
(2)用一平行于![]() 的平面去截这个圆柱,若该截面把圆柱侧面积分成
的平面去截这个圆柱,若该截面把圆柱侧面积分成![]() 两部分,求
两部分,求![]() 与该截面的距离;
与该截面的距离;
(3)求线段![]() ,
,![]() 绕着
绕着![]() 旋转
旋转![]() 所形成的几何体的表面积.
所形成的几何体的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着城市地铁建设的持续推进,市民的出行也越来越便利,根据大数据统计,某条地铁线路运行时,发车时间间隔![]() (单位:分钟)满足:
(单位:分钟)满足: ![]() ,平均每班地铁的载客人数
,平均每班地铁的载客人数![]() (单位:人)与发车时间间隔
(单位:人)与发车时间间隔![]() 近似地满足函数关系:
近似地满足函数关系: ,
,
(1)若平均每班地铁的载客人数不超过1560人,试求发车时间间隔![]() 的取值范围;
的取值范围;
(2)若平均每班地铁每分钟的净收益为![]() (单位:元),则当发车时间间隔
(单位:元),则当发车时间间隔![]() 为多少时,平均每班地铁每分钟的净收益最大?并求出最大净收益.
为多少时,平均每班地铁每分钟的净收益最大?并求出最大净收益.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com