
分析 可设AB中点为D,根据条件AO在∠BAC的平分线上,从而可得到$\overrightarrow{AO}=\frac{k}{2}\overrightarrow{AB}+\frac{k}{3}\overrightarrow{AC}$,而根据D,O,C三点共线及D为AB中点,便可得出$\overrightarrow{AO}=\frac{λ}{2}\overrightarrow{AB}+(1-λ)\overrightarrow{AC}$.从而由平面向量基本定理得到$\left\{\begin{array}{l}{\frac{k}{2}=\frac{λ}{2}}\\{\frac{k}{3}=1-λ}\end{array}\right.$,解出k,便可用$\overrightarrow{AB},\overrightarrow{AC}$表示出$\overrightarrow{AO}$,根据平面向量基本定理即可求出x+y的值.
解答 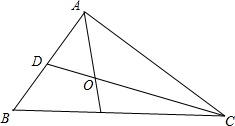 解:如图,设AB中点D;
解:如图,设AB中点D;
∵AO在∠BAC的平分线上,AB=2,AC=3;
∴存在k,使$\overrightarrow{AO}=k(\frac{\overrightarrow{AB}}{2}+\frac{\overrightarrow{AC}}{3})=\frac{k}{2}\overrightarrow{AB}+\frac{k}{3}\overrightarrow{AC}$;
∵D,O,C三点共线,D是AB中点;
∴$\overrightarrow{AO}=λ\overrightarrow{AD}+(1-λ)\overrightarrow{AC}$=$\frac{λ}{2}\overrightarrow{AB}+(1-λ)\overrightarrow{AC}$;
∴由平面向量基本定理得$\left\{\begin{array}{l}{\frac{k}{2}=\frac{λ}{2}}\\{\frac{k}{3}=1-λ}\end{array}\right.$;
解得$k=\frac{3}{4}$;
∴$\overrightarrow{AO}=\frac{3}{8}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$;
又$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}$;
∴$x+y=\frac{3}{8}+\frac{1}{4}=\frac{5}{8}$.
故答案为:$\frac{5}{8}$.
点评 考查向量加法的平行四边形法则,菱形的对角线平分对角,共线向量基本定理,以及平面向量基本定理.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | {3,4,5} | B. | {4,5} | C. | {3,5} | D. | {4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{6}$ | C. | 0或$\frac{1}{6}$ | D. | 0或$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
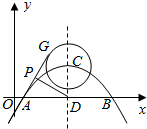 已知抛物线$y=-\frac{3}{16}(x-1)(x-9)$与x轴交于A,B两点,对称轴与抛物线交于点C,与x轴交于点D,⊙C的半径为2,G为⊙C上一动点,P为AG的中点,则DP的最大值为( )
已知抛物线$y=-\frac{3}{16}(x-1)(x-9)$与x轴交于A,B两点,对称轴与抛物线交于点C,与x轴交于点D,⊙C的半径为2,G为⊙C上一动点,P为AG的中点,则DP的最大值为( )| A. | $\frac{7}{2}$ | B. | $\frac{{\sqrt{41}}}{2}$ | C. | $\frac{{\sqrt{34}}}{2}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com