
【题目】某企业为了对生产的一种新产品进行合理定价,将该产品按事先拟定的价格进行试销,得到以下数据:
单价x(元/件) | 60 | 62 | 64 | 66 | 68 | 70 |
销量y(件) | 91 | 84 | 81 | 75 | 70 | 67 |
(I)画出散点图,并求![]() 关于
关于![]() 的回归方程;
的回归方程;
(II)已知该产品的成本是36元/件,预计在今后的销售中,销量与单价仍然服从(I)中的关系,为使企业获得最大利润,该产品的单价应定为多少元(精确到元)?
附:回归直线![]() 的斜率和截距的最小二乘法估计公式分别为:
的斜率和截距的最小二乘法估计公式分别为:
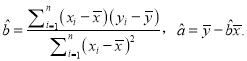
科目:高中数学 来源: 题型:
【题目】天气预报是气象专家根据预测的气象资料和专家们的实际经验,经过分析推断得到的,在现实的生产生活中有着重要的意义,某快餐企业的营销部门对数据分析发现,企业经营情况与降雨填上和降雨量的大小有关.
(1)天气预报所,在今后的三天中,每一天降雨的概率为40%,该营销部分通过设计模拟实验的方法研究三天中恰有两天降雨的概率,利用计算机产生0大9之间取整数值的随机数,并用![]() 表示下雨,其余
表示下雨,其余![]() 个数字表示不下雨,产生了20组随机数:
个数字表示不下雨,产生了20组随机数:
![]()
求由随机模拟的方法得到的概率值;
(2)经过数据分析,一天内降雨量的大小![]() (单位:毫米)与其出售的快餐份数
(单位:毫米)与其出售的快餐份数![]() 成线性相关关系,该营销部门统计了降雨量与出售的快餐份数的数据如下:
成线性相关关系,该营销部门统计了降雨量与出售的快餐份数的数据如下:
![]()
试建立![]() 关于
关于![]() 的回归方程,为尽量满足顾客要求又不在造成过多浪费,预测降雨量为6毫米时需要准备的快餐份数.(结果四舍五入保留整数)
的回归方程,为尽量满足顾客要求又不在造成过多浪费,预测降雨量为6毫米时需要准备的快餐份数.(结果四舍五入保留整数)
附注:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
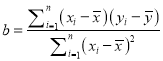 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,过椭圆
中,过椭圆![]() 右焦点的直线
右焦点的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点, ![]() 为
为![]() 的中点,且直线
的中点,且直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设另一直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,原点
两点,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某单位的职工食堂中,食堂每天以![]() 元/个的价格从面包店购进面包,然后以
元/个的价格从面包店购进面包,然后以![]() 元/个的价格出售.如果当天卖不完,剩下的面包以
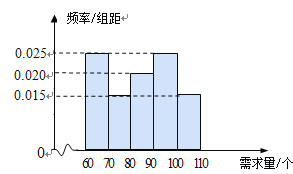
元/个的价格出售.如果当天卖不完,剩下的面包以![]() 元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以
元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以![]() (单位:个,
(单位:个, ![]() )表示面包的需求量,
)表示面包的需求量, ![]() (单位:元)表示利润.
(单位:元)表示利润.
(Ⅰ)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(Ⅱ)根据直方图估计利润![]() 不少于
不少于![]() 元的概率;
元的概率;
(III)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中间值的概率(例如:若需求量![]() ,则取
,则取![]() ,且
,且![]() 的概率等于需求量落入
的概率等于需求量落入![]() 的频率),求
的频率),求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)是R上的偶函数,且当x>0时,函数的解析式为 ![]() .
.
(1)用定义证明f(x)在(0,+∞)上是减函数;
(2)求当x<0时,函数的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且![]()
(1)求证:不论![]() 为何值,总有平面BEF⊥平面ABC;
为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD ?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个![]() 列联表;
列联表;
(2)判断性别与休闲方式是否有关系.
| 0.05 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com