
【题目】已知点![]() 为圆
为圆![]() 的圆心,
的圆心, ![]() 是圆上动点,点
是圆上动点,点![]() 在圆的半径
在圆的半径![]() 上,且有点
上,且有点![]() 和
和![]() 上的点
上的点![]() ,满足
,满足![]()
(1)当![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程;
的轨迹方程;
(2)若斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 相切,与(1)中所求点
相切,与(1)中所求点![]() 的轨迹教育不同的两点
的轨迹教育不同的两点![]()
![]() 是坐标原点,且
是坐标原点,且![]() 时,求
时,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】省环保研究所对某市市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数![]() 与时刻
与时刻![]() (时)的关系为
(时)的关系为 ,其中
,其中![]() 是与气象有关的参数,且
是与气象有关的参数,且![]() ,若用每天
,若用每天![]() 的最大值为当天的综合放射性污染指数,并记作
的最大值为当天的综合放射性污染指数,并记作![]() .
.
(1)令![]() .求
.求![]() 的取值范围;
的取值范围;
(2)求![]() ;
;
(3)省政府规定,每天的综合放射性污染指数不得超过2,试问目前该市市中心的综合放射性污染指数是否超标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,以原点为圆心,椭圆C的短半轴长为半径的圆与直线x﹣y+2=0相切.
,以原点为圆心,椭圆C的短半轴长为半径的圆与直线x﹣y+2=0相切. 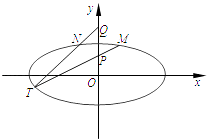
(1)求椭圆C的方程;
(2)已知点P(0,1),Q(0,2).设M,N是椭圆C上关于y轴对称的不同两点,直线PM与QN相交于点T,求证:点T在椭圆C上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司有一款保险产品的历史收益率(收益率=利润÷保费收入)的频率分布直方图如图所示:

(Ⅰ)试估计平均收益率;
(Ⅱ)根据经验,若每份保单的保费在20元的基础上每增加![]() 元,对应的销量
元,对应的销量![]() (万份)与
(万份)与![]() (元)有较强线性相关关系,从历史销售记录中抽样得到如下5组
(元)有较强线性相关关系,从历史销售记录中抽样得到如下5组![]() 与
与![]() 的对应数据:
的对应数据:

据此计算出的回归方程为![]() .
.
(i)求参数![]() 的估计值;
的估计值;
(ii)若把回归方程![]() 当作
当作![]() 与
与![]() 的线性关系,用(Ⅰ)中求出的平均收益率估计此产品的收益率,每份保单的保费定为多少元时此产品可获得最大收益,并求出该最大收益.
的线性关系,用(Ⅰ)中求出的平均收益率估计此产品的收益率,每份保单的保费定为多少元时此产品可获得最大收益,并求出该最大收益.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com