
分析 由点差法结合中点坐标公式和直线的斜率公式,可得直线AB的斜率,求出直线方程,联立直线和椭圆,化为关于x的一元二次方程,利用根与系数关系得到A,B两点的横坐标的和与积,由弦长公式得答案.
解答 解:由P(1,1)在椭圆内,直线AB与椭圆有两个交点.
设A(x1,y1),B(x2,y2),
则$\frac{{{x}_{1}}^{2}}{4}$+$\frac{{{y}_{1}}^{2}}{3}$=1,$\frac{{{x}_{2}}^{2}}{4}$+$\frac{{{y}_{2}}^{2}}{3}$=1,
则$\frac{({x}_{1}+{x}_{2})({x}_{1}-{x}_{2})}{4}$=-$\frac{({y}_{1}-{y}_{2})({y}_{1}+{y}_{2})}{3}$,
即kAB=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{3({x}_{1}+{x}_{2})}{4({y}_{1}+{y}_{2})}$,
由AB中点为P(1,1),即x1+x2=2,y1+y2=2.
知AB的斜率为-$\frac{3}{4}$,且过P(1,1),
则直线AB的方程为y-1=-$\frac{3}{4}$(x-1),即为y=-$\frac{3}{4}$x+$\frac{7}{4}$,
代入椭圆方程,得21x2-42x+1=0.
∴x1+x2=2,x1x2=$\frac{1}{21}$.
∴|AB|=$\sqrt{1+\frac{9}{16}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=
$\frac{5}{4}$•$\sqrt{4-\frac{4}{21}}$=$\frac{5\sqrt{105}}{21}$.
故答案为:$\frac{5\sqrt{105}}{21}$.
点评 本题考查了点差法,涉及直线和圆锥曲线的关系问题,常采用联立直线和圆锥曲线方程,利用根与系数的关系解题,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
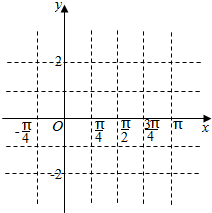 已知函数f(x)=2cosx•sin(x+$\frac{π}{3}$)-$\sqrt{3}$sin2x+sinx•cosx.
已知函数f(x)=2cosx•sin(x+$\frac{π}{3}$)-$\sqrt{3}$sin2x+sinx•cosx.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com