
【题目】已知函数f(x)=2sin( ![]() ﹣φ)(0<φ<
﹣φ)(0<φ< ![]() )的图象经过点(0,﹣1).
)的图象经过点(0,﹣1).
(1)求函数f(x)的对称轴方程及相邻两条对称轴间的距离d;
(2)设α、β∈[0, ![]() ],f(3α+
],f(3α+ ![]() )=
)= ![]() ,f(3β+2π)=
,f(3β+2π)= ![]() ,求cos(α+β)的值.
,求cos(α+β)的值.
【答案】
(1)解:函数f(x)=2sin( ![]() ﹣φ)的图象经过点(0,﹣1),
﹣φ)的图象经过点(0,﹣1),
∴2sin(﹣φ)=﹣1,∴sinφ= ![]() ;
;
又0<φ< ![]() ,
,
∴φ= ![]() ;
;
∴函数f(x)=2sin( ![]() ﹣
﹣ ![]() );
);
令 ![]() ﹣
﹣ ![]() =kπ+
=kπ+ ![]() ,k∈Z,
,k∈Z,
解得x=3kπ+2π,k∈Z,
∴f(x)图象的对称轴方程是x=3kπ+2π,k∈Z;
且相邻两条对称轴间的距离d=(3π+2π)﹣2π=3π
(2)解:由α、β∈[0, ![]() ],f(3α+
],f(3α+ ![]() )=2sinα=
)=2sinα= ![]() ,
,
∴sinα= ![]() ,cosα=
,cosα= ![]() ;
;
f(3β+2π)=2sin(β+ ![]() )=2cosβ=
)=2cosβ= ![]() ,
,
∴cosβ= ![]() ,sinβ=
,sinβ= ![]() ;
;
∴cos(α+β)=cosαcosβ﹣sinαsinβ= ![]() ×
× ![]() ﹣
﹣ ![]() ×
× ![]() =
= ![]()
【解析】(1)根据题意求出函数f(x)的解析式,利用正弦函数的图象性质求出f(x)图象的对称轴方程以及相邻两条对称轴间的距离d;(2)由题意求出sinα、cosα和cosβ、sinβ的值,再计算cos(α+β)的值.


科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问部分职工,根据被访问职工对该部门的评分,绘制频率分布直方图(如图所示).
(1)求频率分布表中①、②、③位置相应数据,并在答题纸上完成频率分布直方图;
组号 | 分组 | 频数 | 频率 |
第1组 | [50,60) | 5 | 0.050 |
第2组 | [60,70) | ① | 0.350 |
第3组 | [70,80) | 30 | ② |
第4组 | [80,90) | 20 | 0.200 |
第5组 | [90,100] | 10 | 0.100 |
合计 | ③ | 1.00 | |
(2)为进一步了解情况,该企业决定在第3,4,5组中用分层抽样抽取5名职工进行座谈,求第3,4,5组中各自抽取的人数;
(3)求该样本平均数 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin2x的图象,只需把函数y=sin(2x﹣ ![]() )的图象( )
)的图象( )
A.向左平移 ![]() 个单位长度
个单位长度
B.向右平移 ![]() 个单位长度
个单位长度
C.向左平移 ![]() 个单位长度
个单位长度
D.向右平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(
=( ![]() sinx,﹣1),
sinx,﹣1), ![]() =(cosx,m),m∈R.
=(cosx,m),m∈R.
(1)若m= ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的值;
的值;
(2)已知函数f(x)=2( ![]() +
+ ![]() )
) ![]() ﹣2m2﹣1,若函数f(x)在[0,
﹣2m2﹣1,若函数f(x)在[0, ![]() ]上有零点,求m的取值范围.
]上有零点,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨),一位居民的月用水量不超过
(吨),一位居民的月用水量不超过![]() 的部分按平价收费,超过
的部分按平价收费,超过![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照![]() ,
, ![]() ,
, ![]() ,
, ![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
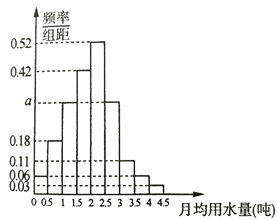
(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)若将频率视为概率,从该城市居民中随机抽取3人,记这3人中月均用水量不低于3吨的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值(精确到0.01),并说明理由.
的值(精确到0.01),并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某休闲农庄有一块长方形鱼塘ABCD,AB=50米,BC=25 ![]() 米,为了便于游客休闲散步,该农庄决定在鱼塘内建三条如图所示的观光走廊OE、EF和OF,考虑到整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°.
米,为了便于游客休闲散步,该农庄决定在鱼塘内建三条如图所示的观光走廊OE、EF和OF,考虑到整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且∠EOF=90°. 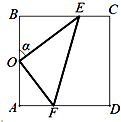
(1)设∠BOE=α,试将△OEF的周长l表示成α的函数关系式,并求出此函数的定义域;
(2)经核算,三条走廊每米建设费用均为4000元,试问如何设计才能使建设总费用最低并求出最低总费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax﹣1,(a为实数),g(x)=lnx﹣x
(1)讨论函数f(x)的单调区间;
(2)求函数g(x)的极值;
(3)求证:lnx<x<ex(x>0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com