
【题目】在四棱锥![]() 中,
中, ![]() 为正三角形,平面
为正三角形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 的体积;
的体积;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,请确定点
?若存在,请确定点![]() 的位置并证明;若不存在,说明理由.
的位置并证明;若不存在,说明理由.
【答案】(1)证明见解析;(2)![]() ;(3)存在,证明见解析.
;(3)存在,证明见解析.
【解析】试题分析:(Ⅰ)先证明![]() ,再根据面面垂直的性质定理可得
,再根据面面垂直的性质定理可得![]() 平面
平面![]() ,再利用面面垂直的判定定理可得结论;(Ⅱ)先根据面面垂直的性质定理可得
,再利用面面垂直的判定定理可得结论;(Ⅱ)先根据面面垂直的性质定理可得![]() 平面
平面![]() ,再根据棱锥的体积公式可得结果;(Ⅲ)
,再根据棱锥的体积公式可得结果;(Ⅲ) ![]() 为
为![]() 的中点时,
的中点时, ![]() 平面
平面![]() ,根先证明平面
,根先证明平面![]() 平面
平面![]() ,从而可得结果.
,从而可得结果.
试题解析:(Ⅰ)因为![]() ,
, ![]() ,
,
所以![]() .
.
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.

(Ⅱ)取![]() 的中点
的中点![]() ,连结
,连结![]() .
.
因为![]() 为正三角形,
为正三角形,
所以![]() .
.
因为平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]()
![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() 为三棱锥
为三棱锥![]() 的高.
的高.
因为![]() 为正三角形,
为正三角形, ![]() ,
,
所以![]() .
.
所以 ![]() .
.
(Ⅲ)在棱![]() 上存在点
上存在点![]() ,当
,当![]() 为
为![]() 的中点时,
的中点时, ![]() 平面
平面![]() .
.
分别取![]() 的中点
的中点![]() ,连结
,连结![]() .
.
所以![]() . 因为
. 因为![]() ,
, ![]() ,
,
所以![]() .
.
所以四边形![]() 为平行四边形.
为平行四边形.
所以![]() .
.
因为![]() ,
,
所以平面![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=|2x﹣1|,定义f1(x)=x,fn+1(x)=f(fn(x)),已知函数g(x)=fm(x)﹣x有8个零点,则m的值为( )
A.8
B.4
C.3
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2lnx,h(x)=x2﹣x+a.
(1)其求函数f(x)的极值;
(2)设函数k(x)=f(x)﹣h(x),若函数k(x)在[1,3]上恰有两个不同零点求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知: ![]() =(2sinx,2cosx),
=(2sinx,2cosx), ![]() =(cosx,﹣cosx),f(x)=
=(cosx,﹣cosx),f(x)= ![]() .
.
(1)若 ![]() 与
与 ![]() 共线,且x∈(
共线,且x∈( ![]() ,π),求x的值;
,π),求x的值;
(2)求函数f(x)的周期;
(3)若对任意x∈[0, ![]() ]不等式m﹣2≤f(x)≤m+
]不等式m﹣2≤f(x)≤m+ ![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我市九龙江南岸江滨路建设的持续推进,未来市民将新增又一休闲好去处,据悉南江滨路建设工程规划配套建造一个长方形公园ABCD,如图所示,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成,已知休闲区A1B1C1D1的面积为4000m2 , 人行道的宽度分别为4m和10m.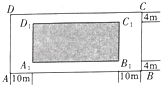
(1)若休闲区的长A1B1=x m,求公园ABCD所占面积S关于x的函数S(x)的解析式;
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败(满分为100分).


(1)求图中![]() 的值;
的值;
(2)估计该次考试的平均分![]() (同一组中的数据用该组的区间中点值代表);
(同一组中的数据用该组的区间中点值代表);
(3)根据已知条件完成下面![]() 列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(参考公式:  ,其中
,其中![]() )
)
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线 ![]() :
: 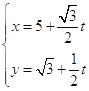 (t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为
(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为 ![]() .
.
(1)将曲线C的极坐标方程化为直坐标方程;
(2)设点M的直角坐标为 ![]() ,直线l与曲线C的交点为A,B,求|MA||MB|的值.
,直线l与曲线C的交点为A,B,求|MA||MB|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com