
【题目】如图所示为一正方体的平面展开图,在这个正方体中,有下列四个命题:
①AF⊥GC;
②BD与GC成异面直线且夹角为60;
③BD∥MN;
④BG与平面ABCD所成的角为45.
其中正确的个数是( )
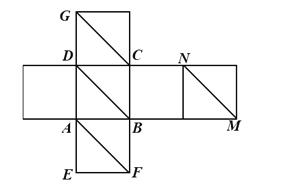
A. 1 B. 2 C. 3 D. 4
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
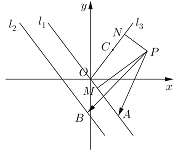
【题目】如图,已知直线![]() 和直线
和直线![]() ,射线
,射线![]() 的一个法向量为
的一个法向量为![]() ,点
,点![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是直线
分别是直线![]() 、
、![]() 上的动点,直线
上的动点,直线![]() 和
和![]() 之间的距离为2,
之间的距离为2,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ;
;
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的最大值;
的最大值;
(3)若![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为4的正方形![]() 中,半径为1的动圆Q的圆心Q在边CD和DA上移动(包含端点A,C,D),P是圆Q上及其内部的动点,设,
中,半径为1的动圆Q的圆心Q在边CD和DA上移动(包含端点A,C,D),P是圆Q上及其内部的动点,设,![]() 则
则![]() 的取值范围是_____________.
的取值范围是_____________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两点![]() 、
、![]() ,动点
,动点![]() 在
在![]() 轴上的射影是
轴上的射影是![]() ,且
,且![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 、
、![]() 的两个斜率存在,分别记为
的两个斜率存在,分别记为![]() 、
、![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若经过点![]() 的直线
的直线![]() 与动点
与动点![]() 的轨迹有两个交点
的轨迹有两个交点![]() 、
、![]() ,当
,当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .以极点为原点,极轴为
.以极点为原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)判断直线![]() 与曲线
与曲线![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若直线![]() 和曲线
和曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学生人均课外学习时间是指单日内学生不在教室内的平均学习时间,这种课外学习时间对学生的学习有一定的影响.合肥市经开区某著名高中学生群体![]() 有走读生和住校生两种,调查显示:当群体
有走读生和住校生两种,调查显示:当群体![]() 中
中![]() 的学生为走读生时,走读生的人均课外学习时间(单位分钟)为
的学生为走读生时,走读生的人均课外学习时间(单位分钟)为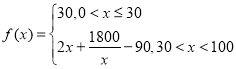 ,而住校生的人均课外学习时间恒为40分钟,试根据上述调查结果回答下列问题:
,而住校生的人均课外学习时间恒为40分钟,试根据上述调查结果回答下列问题:
(1)当![]() 为何值时,住校生的人均课外学习时间等于走读生的课外人均学习时间?
为何值时,住校生的人均课外学习时间等于走读生的课外人均学习时间?
(2)求该校高中学生群体![]() 的人均课外学习时间
的人均课外学习时间![]() 的表达式,并求
的表达式,并求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com