
【题目】已知数列{an}的前n项和为Sn , 且Sn=2an﹣3n(n∈N+).
(1)求a1 , a2 , a3的值;
(2)设bn=an+3,证明数列{bn}为等比数列,并求通项公式an .
【答案】
(1)解:∵数列{an}的前n项和为Sn,且Sn=2an﹣3n(n∈N+).
∴n=1时,由a1=S1=2a1﹣3×1,解得a1=3,
n=2时,由S2=2a2﹣3×2,得a2=9,
n=3时,由S3=2a3﹣3×3,得a3=21.
(2)解:∵Sn=2an﹣3×n,∴Sn+1=2an+1﹣3×(n+1),
两式相减,得an+1=2an+3,*
把bn=an+3及bn+1=an+1+3,代入*式,
得bn+1=2bn,(n∈N*),且b1=6,
∴数列{bn}是以6为首项,2为公比的等比数列,
∴bn=6×2n﹣1,
∴ ![]() .
.
【解析】(1)根据递推公式Sn=2an﹣3n,可求出所求值,(2)由Sn=2an﹣3×n,则Sn+1=2an+1﹣3×(n+1),两式相减得an+1=2an+3,将bn代入可得bn+1=2bn,数列{bn}是以6为首项,2为公比的等比数列bn=6×2n﹣1,a n = b n 3= 3 ( 2 n 1 ) .
【考点精析】利用等比数列的通项公式(及其变式)和数列的前n项和对题目进行判断即可得到答案,需要熟知通项公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系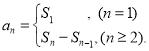 .
.


科目:高中数学 来源: 题型:
【题目】在正方体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体是(写出所有正确结论的编号).
①矩形;
②不是矩形的平行四边形;
③有三个面为等腰直角三角形,有一个面为等边三角形的四面体;
④每个面都是等边三角形的四面体;
⑤每个面都是直角三角形的四面体.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】凸函数的性质定理为:如果函数f(x)在区间D上是凸函数,则对于区间D内的任意x1 , x2 , …,xn , 有 ![]() ≤f(
≤f( ![]() ),已知函数y=sinx在区间(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值为
),已知函数y=sinx在区间(0,π)上是凸函数,则在△ABC中,sinA+sinB+sinC的最大值为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1: ![]() +x2=1(a>1)与抛物线C
+x2=1(a>1)与抛物线C ![]() :x2=4y有相同焦点F1 .
:x2=4y有相同焦点F1 .
(Ⅰ)求椭圆C1的标准方程;
(Ⅱ)已知直线l1过椭圆C1的另一焦点F2 , 且与抛物线C2相切于第一象限的点A,设平行l1的直线l交椭圆C1于B,C两点,当△OBC面积最大时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设x∈R,记不超过x的最大整数为[x],例如[2.34]=2,[﹣1.5]=﹣2,令{x}=x﹣[x],则 ![]() ( )
( )
A.是等差数列但不是等比数列
B.既是等差数列也是等比数列
C.是等比数列但不是等差数列
D.既不是等差数列也不是等比数列
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com