
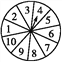
【题目】有一个转盘游戏,转盘被平均分成10等份(如图所示),转动转盘,当转盘停止后,指针指向的数字即为转出的数字.游戏规则如下:两个人参加,先确定猜数方案,甲转动转盘,乙猜,若猜出的结果与转盘转出的数字所表示的特征相符,则乙获胜,否则甲获胜.猜数方案从以下三种方案中选一种:
A.猜“是奇数”或“是偶数”
B.猜“是4的整数倍数”或“不是4的整数倍数”
C.猜“是大于4的数”或“不是大于4的数”
请回答下列问题:
(1)如果你是乙,为了尽可能获胜,你将选择哪种猜数方案,并且怎样猜?为什么?
(2)为了保证游戏的公平性,你认为应制定哪种猜数方案?为什么?
(3)请你设计一种其他的猜数方案,并保证游戏的公平性.
【答案】(1) 应选方案B ,猜“不是4的整数倍数”;(2) 应当选择方案A;
(3) 可以设计为:猜“是大于5的数”或“不是大于5的数”
【解析】试题分析:(1) 方案A中“是奇数”或“是偶数”的概率均为![]() ,案B中“不是4的整数倍数”的概率为
,案B中“不是4的整数倍数”的概率为![]() ,“是4的整数倍数”的概率为
,“是4的整数倍数”的概率为![]() ,方案C中“是大于4的数”的概率为
,方案C中“是大于4的数”的概率为![]() ,“不是大于4的数”的概率为
,“不是大于4的数”的概率为![]() ,乙为了尽可能获胜,应选方案B,猜“不是4的整数倍数”. (2) 为了保证游戏的公平性,应当选择方案A. “是奇数”或“是偶数”的概率均为
,乙为了尽可能获胜,应选方案B,猜“不是4的整数倍数”. (2) 为了保证游戏的公平性,应当选择方案A. “是奇数”或“是偶数”的概率均为![]() (3) “是大于5的数”或“不是大于5的数”发生的概率是一样的,也可以保证游戏的公平性
(3) “是大于5的数”或“不是大于5的数”发生的概率是一样的,也可以保证游戏的公平性
试题解析:
(1)如题图,方案A中“是奇数”或“是偶数”的概率均为![]() =0.5;方案B中“不是4的整数倍数”的概率为
=0.5;方案B中“不是4的整数倍数”的概率为![]() =0.8,“是4的整数倍数”的概率为
=0.8,“是4的整数倍数”的概率为![]() =0.2;方案C中“是大于4的数”的概率为
=0.2;方案C中“是大于4的数”的概率为![]() =0.6,“不是大于4的数”的概率为
=0.6,“不是大于4的数”的概率为![]() =0.4.乙为了尽可能获胜,应选方案B,猜“不是4的整数倍数”.
=0.4.乙为了尽可能获胜,应选方案B,猜“不是4的整数倍数”.
(2)为了保证游戏的公平性,应当选择方案A.因为方案A猜“是奇数”或“是偶数”的概率均为0.5,从而保证了该游戏是公平的.
(3)可以设计为:猜“是大于5的数”或“不是大于5的数”,此方案也可以保证游戏的公平性.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】某市的3个区共有高中学生20 000人,且3个区的高中学生人数之比为2∶3∶5,现要从所有学生中抽取一个容量为200的样本,调查该市高中学生的视力情况,试写出抽样过程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人做游戏,下列游戏不公平的是( )
A. 抛掷一枚骰子,向上的点数为奇数则甲获胜,向上的点数为偶数则乙获胜
B. 同时抛掷两枚硬币,恰有一枚正面向上则甲获胜,两枚都正面向上则乙获胜
C. 从一副不含大小王的扑克牌中抽一张,扑克牌是红色的则甲获胜,扑克牌是黑色的则乙获胜
D. 甲、乙两人各写一个数字1或2,如果两人写的数字相同甲获胜,否则乙获胜
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)在如图所示的五面体中,面![]() 为直角梯形,
为直角梯形, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是边长为2的正三角形.
是边长为2的正三角形.
(1)证明: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下五个命题:
①在线性回归模型中, ![]() 表示解释变量对于预报变量变化的贡献率,在对女大学生的身高预报体重的回归分析数据中,算得
表示解释变量对于预报变量变化的贡献率,在对女大学生的身高预报体重的回归分析数据中,算得![]() ,表明“女大学生的体重差异有64%是由身高引起的”
,表明“女大学生的体重差异有64%是由身高引起的”
②随机变量的方差和标准差都反映了随机变量取值偏离于均值的平均程度,方差或标准差越小,则随机变量偏离于均值的平均程度越大;
③正态曲线关于直线![]() 对称,这个曲线只有当
对称,这个曲线只有当![]() 时,才在
时,才在![]() 轴上方;
轴上方;
④正态曲线的对称轴由![]() 确定,当
确定,当![]() 一定时,曲线的形状由
一定时,曲线的形状由![]() 决定,并且
决定,并且![]() 越大,曲线越“矮胖”;
越大,曲线越“矮胖”;
⑤若随机变量![]() ,且
,且![]() 则
则![]() ;
;
其中正确命题的序号是
A. ②③ B. ①④⑤ C. ①④ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代名词“刍童”原来是草堆的意思,古代用它作为长方体棱台(上、下底面均为矩形额棱台)的专用术语,关于“刍童”体积计算的描述,《九章算术》注曰:“倍上表,下表从之,亦倍小表,上表从之,各以其广乘之,并,以高若深乘之,皆六面一.”其计算方法是:将上底面的长乘二,与下底面的长相加,再与上底面的宽相乘;将下底面的长乘二,与上底面的长相加,再与下底面的宽相乘;把这两个数值相加,与高相乘,再取其六分之一,以此算法,现有上下底面为相似矩形的棱台,相似比为![]() ,高为3,且上底面的周长为6,则该棱台的体积的最大值是( )
,高为3,且上底面的周长为6,则该棱台的体积的最大值是( )
A. 14 B. 56 C. ![]() D. 63
D. 63
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O1和圆O2的极坐标方程分别为ρ=2,ρ2-2![]() ρcos(θ-
ρcos(θ-![]() )=2.
)=2.
(1)把圆O1和圆O2的极坐标方程化为直角坐标方程;
(2)设两圆交点分别为A、B,求直线AB的参数方程,并利用直线AB的参数方程求两圆的公共弦长|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() ),以椭圆内一点
),以椭圆内一点![]() 为中点作弦
为中点作弦![]() ,设线段
,设线段![]() 的中垂线与椭圆相交于
的中垂线与椭圆相交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆的离心率;
(Ⅱ)试判断是否存在这样的![]() ,使得
,使得![]() ,
, ![]() ,
, ![]() ,
, ![]() 在同一个圆上,并说明理由.
在同一个圆上,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com