
【题目】学习了余弦定理后,老师布置了一个课外任务,让同学们自己制作一些直角三角形、锐角三角形或钝角三角形的模型,现在李明和王强同学已经有了两根长度分别为![]() 和
和![]() 的铁丝.
的铁丝.
(1)如果他们希望能够制作一个直角三角形,那么他们需要的第三根铁丝的长度应该是多少?
(2)如果他们希望能够制作一个钝角三角形,那么他们需要的第三根铁丝的长度应该在什么范围?制作一个锐角三角形呢?
【答案】(1)![]() 或
或![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)分两种情况讨论,斜边为长度为![]() 的铁丝或第三根铁丝,利用勾股定理即可求出结果;
的铁丝或第三根铁丝,利用勾股定理即可求出结果;
(2)若三角形为钝角三角形,分两种情况讨论,最长边为长度为![]() 的铁丝或第三根铁丝,利用最大角的余弦值为负数,结合余弦定理以及三角形三边关系可求得结果,同理可得出当三角形为锐角三角形时第三边长度的取值范围.
的铁丝或第三根铁丝,利用最大角的余弦值为负数,结合余弦定理以及三角形三边关系可求得结果,同理可得出当三角形为锐角三角形时第三边长度的取值范围.
(1)制作一个直角三角形,设第三根铁丝的长度为![]() .
.
①若长度为![]() 的铁丝为斜边,则
的铁丝为斜边,则![]() ;
;
②第三根铁丝为斜边,则![]() .
.
综上所述,所求第三边的长度为![]() 或
或![]() ;
;
(2)制作一个钝角三角形,设第三根铁丝的长度为![]() ,设钝角三角形的最大角为
,设钝角三角形的最大角为![]() .
.
①若最长边为![]() 的铁丝,则
的铁丝,则![]() ,解得
,解得![]() ,
,
又![]() ,
,![]() ,即
,即![]() ;
;
②若最长边为![]() 的铁丝,则
的铁丝,则![]() ,解得
,解得![]() ,
,
由![]() ,此时
,此时![]() .
.
综上所述,当三角形为钝角三角形时,第三边的取值范围是![]() .
.
同理可知,制作一个锐角三角形时,第三边的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为x、y,设O为坐标原点,点P的坐标为![]() 记
记![]() .
.
(1)求随机变量![]() 的最大值,并求事件“
的最大值,并求事件“![]() 取得最大值”的概率;
取得最大值”的概率;
(2)求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年推出一种新型家用轿车,购买时费用为16.9万元,每年应交付保险费、养路费及汽油费共1.2万元,汽车的维修费为:第一年无维修费用,第二年为0.2万元,从第三年起,每年的维修费均比上一年增加0.2万元.
(I)设该辆轿车使用n年的总费用(包括购买费用、保险费、养路费、汽油费及维修费)为f(n),求f(n)的表达式;
(II)这种汽车使用多少报废最合算(即该车使用多少年,年平均费用最少)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]() ,数列
,数列![]() 中,
中,![]() ,对任意正整数
,对任意正整数![]() ,
,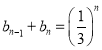 .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)是否存在实数![]() ,使得数列
,使得数列![]() 是等比数列?若存在,请求出实数
是等比数列?若存在,请求出实数![]() 及公比q的值,若不存在,请说明理由;
及公比q的值,若不存在,请说明理由;
(3)求数列![]() 前n项和
前n项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆C的标准方程;
(2)点P是椭圆上异于短轴端点A,B的任意一点,过点P作![]() 轴于Q,线段PQ的中点为M.直线AM与直线
轴于Q,线段PQ的中点为M.直线AM与直线![]() 交于点N,D为线段BN的中点,设O为坐标原点,试判断以OD为直径的圆与点M的位置关系.
交于点N,D为线段BN的中点,设O为坐标原点,试判断以OD为直径的圆与点M的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆O:![]() 和点
和点![]() ,由圆O外一点P向圆O引切线
,由圆O外一点P向圆O引切线![]() ,Q为切点,且有
,Q为切点,且有![]() .
.

(1)求点P的轨迹方程,并说明点P的轨迹是什么样的几何图形?
(2)求![]() 的最小值;
的最小值;
(3)以P为圆心作圆,使它与圆O有公共点,试在其中求出半径最小的圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com