
【题目】如图,在四棱锥P-ABCD中,底面为正方形,△PAD为等边三角形,平面PAD丄平面PCD.
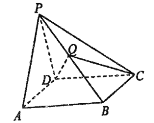
(1)证明:平面PAD丄平面ABCD:
(2)若AB=2,Q为线段的中点,求三棱锥Q-PCD的体积.
【答案】(1)详见解析(2)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,连结
,连结![]() ,利用面面垂直的性质,证得
,利用面面垂直的性质,证得![]() 平面
平面![]() ,再由正方形的性质,证得
,再由正方形的性质,证得![]() ,利用线面垂直的判定定理,得到
,利用线面垂直的判定定理,得到![]() 平面
平面![]() ,进而得到平面
,进而得到平面![]() 平面
平面![]() ;
;
(2)由(1)得![]() 到平面
到平面![]() 的距离
的距离![]() ,进而求得
,进而求得![]() 到平面
到平面![]() 的距离
的距离![]() ,利用体积公式,即可求解.
,利用体积公式,即可求解.
(1)证明:取![]() 的中点
的中点![]() ,连结
,连结![]() ,
,
因为![]() 为等边三角形,所以
为等边三角形,所以![]() ,
,
又因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为底面![]() 为正方形,所以
为正方形,所以![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)由(1)得![]() 平面
平面![]() ,所以
,所以![]() 到平面
到平面![]() 的距离
的距离![]() ,
,
因为底面![]() 为正方形,所以
为正方形,所以![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() 两点到平面
两点到平面![]() 的距离相等,均为
的距离相等,均为![]() ,
,
又![]() 为线段
为线段![]() 的中点,所以
的中点,所以![]() 到平面
到平面![]() 的距离
的距离![]() ,
,
由(1)知,![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() )的最小周期为
)的最小周期为![]() .
.
(1)求![]() 的值及
的值及![]() 的单调递增区间;
的单调递增区间;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,再将图象上各点的横坐标缩短为原来的
个单位,再将图象上各点的横坐标缩短为原来的![]() (纵坐标不变)得到函数
(纵坐标不变)得到函数![]() 的图象,若关于x的方程
的图象,若关于x的方程![]() 在区间
在区间![]() 上有且只有一个解,求实数m的取值范围.
上有且只有一个解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
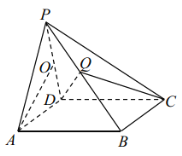
【题目】已知四棱锥![]() 中,底面
中,底面![]() 为菱形,且
为菱形,且![]() ,
,![]() ,过侧面
,过侧面![]() 中线
中线![]() 的一个平面
的一个平面![]() 与直线
与直线![]() 垂直,并与此四棱锥的面相交,交线围成一个平面图形.
垂直,并与此四棱锥的面相交,交线围成一个平面图形.
(1)画出这个平面图形,并证明![]() 平面
平面![]() ;
;
(2)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(|x|﹣b)2+c,函数g(x)=x+m.
(1)当b=2,m=﹣4时,f(x)≥g(x)恒成立,求实数c的取值范围;
(2)当c=﹣3,m=﹣2时,方程f(x)=g(x)有四个不同的解,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了更好地支持“中小型企业”的发展,某市决定对部分企业的税收进行适当的减免,某机构调查了当地的中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,下面三个结论:
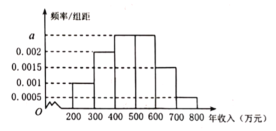
①样本数据落在区间![]() 的频率为0.45;
的频率为0.45;
②如果规定年收入在500万元以内的企业才能享受减免税政策,估计有55%的当地中小型企业能享受到减免税政策;
③样本的中位数为480万元.
其中正确结论的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]()
![]() 的长轴长为4,离心率为
的长轴长为4,离心率为![]() ,点P在椭圆C上.
,点P在椭圆C上.
(1)求椭圆C的标准方程;
(2)已知点M (4,0),点N(0,n),若以PM为直径的圆恰好经过线段PN的中点,求n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国个人所得税法》规定,公民月收入总额(工资、薪金等)不超过免征额的部分不必纳税,超过免征额的部分为全月应纳税所得额,个人所得税税款按税率表分段累计计算.为了给公民合理减负,稳步提升公民的收入水平,自2018年10月1日起,个人所得税免征额和税率进行了调整,调整前后的个人所得税税率表如下:

(1)已知小李2018年9月份上交的税费是295元,10月份月工资、薪金等税前收入与9月份相同,请帮小李计算一下税率调整后小李10月份的税后实际收入是多少?
(2)某税务部门在小李所在公司利用分层抽样方法抽取某月100位不同层次员工的税前收入,并制成下面的频率分布直方图.
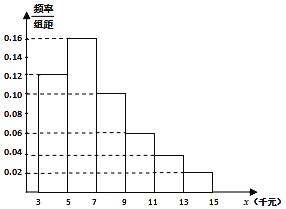
(ⅰ)请根据频率分布直方图估计该公司员工税前收入的中位数;
(ⅱ)同一组中的数据以这组数据所在区间中点的值作代表,按调整后税率表,试估计小李所在的公司员工该月平均纳税多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,称
,称![]() (其中
(其中![]() )为数列
)为数列![]() 的前k项“波动均值”.若对任意的
的前k项“波动均值”.若对任意的![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 为“趋稳数列”.
为“趋稳数列”.
(1)若数列1,![]() ,2为“趋稳数列”,求
,2为“趋稳数列”,求![]() 的取值范围;
的取值范围;
(2)若各项均为正数的等比数列![]() 的公比
的公比![]() ,求证:
,求证:![]() 是“趋稳数列”;
是“趋稳数列”;
(3)已知数列![]() 的首项为1,各项均为整数,前
的首项为1,各项均为整数,前![]() 项的和为
项的和为![]() . 且对任意
. 且对任意![]() ,都有
,都有![]() , 试计算:
, 试计算:![]() (
(![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com