
【题目】已知各项均不相等的等差数列{an}的前四项和S4=14,且a1 , a3 , a7成等比数列. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设Tn为数列{ ![]() }的前n项和,若Tn≤λan+1对n∈N*恒成立,求实数λ的最小值.
}的前n项和,若Tn≤λan+1对n∈N*恒成立,求实数λ的最小值.
【答案】解:(I)设公差为d,由已知得: 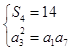 , 即
, 即 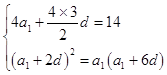 ,
,
解得:d=1或d=0(舍去),
∴a1=2,
故an=2+(n﹣1)=n+1;
(II)∵ ![]() =
= ![]() ,
,
∴Tn= ![]() ,
,
∵Tn≤λan+1对n∈N*恒成立,即 ![]() ≤λ(n+2),λ≥
≤λ(n+2),λ≥ ![]() n∈N*恒成立,
n∈N*恒成立,
又 ![]() =
= 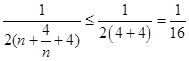 ,
,
∴λ的最小值为 ![]() .
.
【解析】(I)设出此等差数列的公差为d,根据等差数列的前n项和公式化简S4=14得到关于首项和公差的关系式,又a1 , a3 , a7成等比数列,根据等比数列的性质得到关于首项和公差的另一关系式,两关系式联立即可求出首项和公差,根据首项和公差写出等差数列{an}的通项公式即可;(II)把(I)中求出的数列{an}的通项公式代入数列中,根据 ![]() ,列举出数列的前n项和的每一项,抵消后得到Tn的通项公式,将求出的Tn的通项公式和an+1的通项公式代入已知的不等式中,解出λ大于等于一个关系式,利用基本不等式求出这个关系式的最大值,即可得到实数λ的最小值.
,列举出数列的前n项和的每一项,抵消后得到Tn的通项公式,将求出的Tn的通项公式和an+1的通项公式代入已知的不等式中,解出λ大于等于一个关系式,利用基本不等式求出这个关系式的最大值,即可得到实数λ的最小值.


科目:高中数学 来源: 题型:
【题目】为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00~10:00各自的点击量,得到如图所示的茎叶图,根据茎叶图回答下列问题.

(1)甲、乙两个网站点击量的极差分别是多少?
(2)甲网站点击量在[10,40]间的频率是多少?
(3)甲、乙两网站哪个更受欢迎?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合P的元素个数为![]() 个且元素为正整数,将集合P分成元素个数相同且两两没有公共元素的三个集合A、B、C,即
个且元素为正整数,将集合P分成元素个数相同且两两没有公共元素的三个集合A、B、C,即![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]()
![]() ,
,![]() ,
,![]()
![]() 若集合A、B、C中的元素满足
若集合A、B、C中的元素满足![]()
![]() ,
,![]() ,
,![]() ,2,
,2,![]() ,则称集合P为“完美集合”.
,则称集合P为“完美集合”.
![]() 若集合
若集合![]() 2,
2,![]() ,
,![]() 2,3,4,5,
2,3,4,5,![]() ,判断集合P和集合Q是否为“完美集合”?并说明理由;
,判断集合P和集合Q是否为“完美集合”?并说明理由;
![]() 已知集合
已知集合![]() x,3,4,5,
x,3,4,5,![]() 为“完美集合”,求正整数x的值;
为“完美集合”,求正整数x的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:![]() ,直线l:
,直线l:![]() ,A为直线l上一点.
,A为直线l上一点.
![]() 若
若![]() ,过A作圆M的两条切线,切点分别为P,Q,求
,过A作圆M的两条切线,切点分别为P,Q,求![]() 的大小;
的大小;
![]() 若圆M上存在两点B,C,使得
若圆M上存在两点B,C,使得![]() ,求点A横坐标的取值范围.
,求点A横坐标的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知cos(α﹣β)=﹣ ![]() ,cos(α+β)=
,cos(α+β)= ![]() ,且(α﹣β)∈(
,且(α﹣β)∈( ![]() ,π),(α+β)∈(
,π),(α+β)∈( ![]() ,2π),则cos2α=( )
,2π),则cos2α=( )
A.﹣1
B.﹣ ![]()
C.![]()
D.﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sin2x+
sin2x+ ![]() sin2x.
sin2x.
(1)求函数f(x)的单调递减区间;
(2)在△ABC中,角A,B,C的对边分别为a,b,c,若f( ![]() )=
)= ![]() ,△ABC的面积为3
,△ABC的面积为3 ![]() ,求a的最小值.
,求a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函f(x)=ax2﹣ex(a∈R). (Ⅰ)a=1时,试判断f(x)的单调性并给予证明;
(Ⅱ)若f(x)有两个极值点x1 , x2(x1<x2).
(i) 求实数a的取值范围;
(ii)证明:﹣ ![]() . (注:e是自然对数的底数)
. (注:e是自然对数的底数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆 ![]() +
+ ![]() =1(a>b>0)的左右焦点分别为F1 , F2 , 点D在椭圆上,DF1⊥F1F2 ,
=1(a>b>0)的左右焦点分别为F1 , F2 , 点D在椭圆上,DF1⊥F1F2 , ![]() =2
=2 ![]() ,△DF1F2的面积为
,△DF1F2的面积为 ![]() . (Ⅰ)求该椭圆的标准方程;
. (Ⅰ)求该椭圆的标准方程;
(Ⅱ)是否存在圆心在y轴上的圆,使圆在x轴的上方与椭圆有两个交点,且圆在这两个交点处的两条切线互相垂直并分别过不同的焦点?若存在,求出圆的方程;若不存在,请说明理由.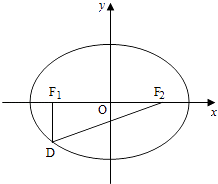
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com