
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源:不详 题型:解答题
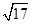 ,求直线l的倾斜角;
,求直线l的倾斜角;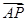 =
=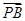 ,求此时直线l的方程.
,求此时直线l的方程.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
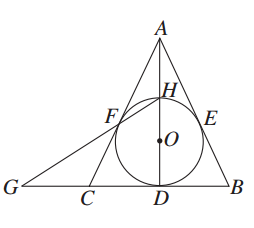
 ,∠APB=30°,则AE=________.
,∠APB=30°,则AE=________.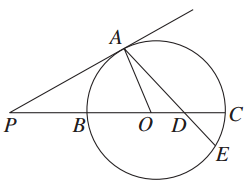
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
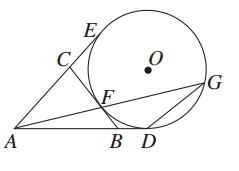
| A.①② | B.②③ | C.①③ | D.①②③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
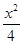 +y2=1.过
+y2=1.过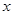 轴上的动点
轴上的动点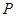 (m,0)作圆x2+y2=1的切线l交椭圆G于A,B两点.
(m,0)作圆x2+y2=1的切线l交椭圆G于A,B两点.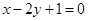 的最大距离;
的最大距离; 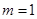 时,求A,B两点坐标;
时,求A,B两点坐标;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 有公共点,则b的取值范围是( )
有公共点,则b的取值范围是( )A.[1-2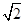 ,1+2 ,1+2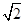 ] ] | B.[1-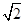 ,3] ,3] |
C.[-1,1+2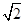 ] ] | D.[1-2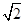 ,3] ,3] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com