
【题目】口袋里装有1红,2白,3黄共6个形状相同的小球,从中取出2球,事件![]() “取出的两球同色”,
“取出的两球同色”,![]() “取出的2球中至少有一个黄球”,
“取出的2球中至少有一个黄球”,![]() “取出的2球至少有一个白球”,
“取出的2球至少有一个白球”,![]() “取出的两球不同色”,
“取出的两球不同色”,![]() “取出的2球中至多有一个白球”.下列判断中正确的序号为________.
“取出的2球中至多有一个白球”.下列判断中正确的序号为________.
①![]() 与
与![]() 为对立事件;②
为对立事件;②![]() 与
与![]() 是互斥事件;③
是互斥事件;③![]() 与
与![]() 是对立事件:④
是对立事件:④![]() ;⑤
;⑤![]() .
.
【答案】①④
【解析】
在①中,由对立事件定义得![]() 与
与![]() 为对立事件;有②中,
为对立事件;有②中,![]() 与
与![]() 有可能同时发生;在③中,
有可能同时发生;在③中,![]() 与
与![]() 有可能同时发生;在④中,
有可能同时发生;在④中,![]() (C)
(C)![]() (E)
(E)![]() ;在⑤中
;在⑤中![]() ,从而
,从而![]() (B)
(B)![]() (C).
(C).
![]() 口袋里装有1红,2白,3黄共6个形状相同小球,从中取出2球,
口袋里装有1红,2白,3黄共6个形状相同小球,从中取出2球,
事件![]() “取出的两球同色”,
“取出的两球同色”, ![]() “取出的2球中至少有一个黄球”,
“取出的2球中至少有一个黄球”,
![]() “取出的2球至少有一个白球”,
“取出的2球至少有一个白球”, ![]() “取出的两球不同色”,
“取出的两球不同色”, ![]() “取出的2球中至多有一个白球”,
“取出的2球中至多有一个白球”,
①,由对立事件定义得![]() 与
与![]() 为对立事件,故①正确;
为对立事件,故①正确;
②,![]() 与
与![]() 有可能同时发生,故
有可能同时发生,故![]() 与
与![]() 不是互斥事件,故②错误;
不是互斥事件,故②错误;
③,![]() 与
与![]() 有可能同时发生,不是对立事件,故③错误;
有可能同时发生,不是对立事件,故③错误;
④,![]() (C)
(C)![]() ,
,![]() (E)
(E)![]() ,
,![]() ,
,
从而![]() (C)
(C)![]() (E)
(E)![]() ,故④正确;
,故④正确;
⑤,![]() ,从而
,从而![]() (B)
(B)![]() (C),故⑤错误.
(C),故⑤错误.
故答案为:①④.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:
【题目】某农科所发现,一种作物的年收获量![]() (单位:
(单位:![]() )与它“相近”作物的株数
)与它“相近”作物的株数![]() 具有相关关系(所谓两株作物“相近”是指它们的直线距离不超过
具有相关关系(所谓两株作物“相近”是指它们的直线距离不超过![]() ),并分别记录了相近作物的株数为
),并分别记录了相近作物的株数为![]() 时,该作物的年收获量的相关数据如下:
时,该作物的年收获量的相关数据如下:
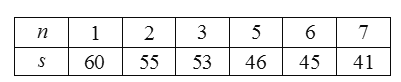
(1)根据研究发现,该作物的年收获量![]() 可能和它“相近”作物的株数
可能和它“相近”作物的株数![]() 有以下两种回归方程:
有以下两种回归方程:![]() ,利用统计知识,结合相关系数
,利用统计知识,结合相关系数![]() 比较使用哪种回归方程更合适;
比较使用哪种回归方程更合适;
(2)农科所在如下图所示的正方形地块的每个格点(指纵、横直线的交叉点)处都种了一株该作物,其中每个小正方形的面积为![]() ,若在所种作物中随机选取一株,求它的年收获量的分布列与数学期望.(注:年收获量以(1)中选择的回归方程计算所得数据为依据)
,若在所种作物中随机选取一株,求它的年收获量的分布列与数学期望.(注:年收获量以(1)中选择的回归方程计算所得数据为依据)
参考公式:线性回归方程为![]() ,其中
,其中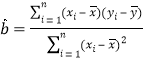 ,
,![]() ,
,
相关系数 ;
;
参考数值:![]() ,
,![]() ,
,![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某教育主管部门到一所中学检查高三年级学生的体质健康情况,从中抽取了![]() 名学生的体质测试成绩,得到的频率分布直方图如图1所示,样本中前三组学生的原始成绩按性别分类所得的茎叶图如图2所示.
名学生的体质测试成绩,得到的频率分布直方图如图1所示,样本中前三组学生的原始成绩按性别分类所得的茎叶图如图2所示.
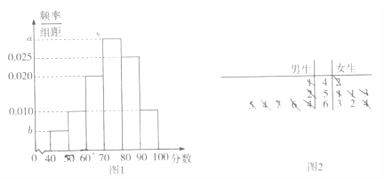
(Ⅰ)求![]() ,
, ![]() ,
, ![]() 的值;
的值;
(Ⅱ)估计该校高三学生体质测试成绩的平均数![]() 和中位数
和中位数![]() ;
;
(Ⅲ)若从成绩在![]() 的学生中随机抽取两人重新进行测试,求至少有一名男生的概率.
的学生中随机抽取两人重新进行测试,求至少有一名男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴为极轴建立极坐标系,曲线
轴为极轴建立极坐标系,曲线![]() 的极坐标为
的极坐标为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 和曲线
和曲线![]() 有三个公共点,求以这三个公共点为顶点的三角形的面积.
有三个公共点,求以这三个公共点为顶点的三角形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正整数数列中,由1开始依次按如下规则,将某些整数染成红色,先染1;再染3个偶数2,4,6;再染6后面最邻近的5个连续奇数7,9,11,13,15;再染15后面最邻近的7个连续偶数16,18,20,22,24,26,28;再染此后最邻近的9个连续奇数29,31,…,45;按此规则一直染下去,得到一红色子数列:1,2,4,6,7,9,11,13,15,16,……,则在这个红色子数列中,由1开始的第2019个数是( )
A. 3972 B. 3974 C. 3991 D. 3993
查看答案和解析>>
科目:高中数学 来源: 题型:
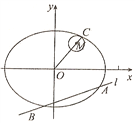
【题目】如图所示,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的中心在原点,点
的中心在原点,点![]() 在椭圆
在椭圆![]() 上,且离心率为
上,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)动直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,
两点, ![]() 是椭圆
是椭圆![]() 上一点,直线
上一点,直线![]() 的斜率为
的斜率为![]() ,且
,且![]() ,
, ![]() 是线段
是线段![]() 上一点,圆
上一点,圆![]() 的半径为
的半径为![]() ,且
,且![]() ,求
,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(![]() ,
,![]() )
)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com