
【题目】已知函数f(x)=2lnx+ax﹣ ![]() (a∈R)在x=2处的切线经过点(﹣4,2ln2)
(a∈R)在x=2处的切线经过点(﹣4,2ln2)
(1)讨论函数f(x)的单调性
(2)若不等式 ![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
【答案】
(1)解:由f(x)=2lnx+ax﹣ ![]() (a∈R),求导f′(x)=
(a∈R),求导f′(x)= ![]() +a+
+a+ ![]() ,
,
当x=2时,f′(2)=1+a+f′(2),
∴a=﹣1,
设切点为(2,2ln2+2a﹣2f′(2)),则切线方程y﹣(2ln2+2a﹣2f′(2))=f′(2)(x﹣2),
将(﹣4,2ln2)代入切线方程,2ln2﹣2ln2﹣2a+2f′(2))=﹣6f′(2),则f′(2)=﹣ ![]() ,
,
∴f′(x)= ![]() ﹣1﹣
﹣1﹣ ![]() =
= ![]() ≤0,
≤0,
∴f(x)在(0,+∞)单调递减
(2)解:由不等式 ![]() 恒成立,则
恒成立,则 ![]() (2lnx+
(2lnx+ ![]() )>m,
)>m,
令φ(x)=2lnx+ ![]() ,(x>0)求导φ′(x)=
,(x>0)求导φ′(x)= ![]() ﹣
﹣ ![]() ﹣1=﹣(
﹣1=﹣( ![]() ﹣1)2≤0,
﹣1)2≤0,
∴φ(x)在(0,+∞)单调递减,
由φ(1)=0,
则当0<x<1时,φ(x)>0,
当x>1时,φ(x)<0,
∴ ![]() (2lnx+
(2lnx+ ![]() )在(0,+∞)恒大于0,
)在(0,+∞)恒大于0,
∴m≤0,
实数m的取值范围(﹣∞,0]
【解析】(1)求导,当x=2时,代入f′(x),即可求得a=﹣1,求得点斜式方程,将(﹣4,2ln2)代入点斜式方程,即可求得f′(2),即可求得函数f(x)的单调区间;(2)由题意可知 ![]() (2lnx+
(2lnx+ ![]() )>m,构造辅助函数,求导,根据函数的单调性及零点性质,求得
)>m,构造辅助函数,求导,根据函数的单调性及零点性质,求得 ![]() (2lnx+
(2lnx+ ![]() )最小值,即可求得实数m的取值范围.
)最小值,即可求得实数m的取值范围.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】下面四个命题中,真命题是( ) ①从匀速传递的产品生产流水线上,质检员每30分钟从生产流水线中抽取一件产品进行某项指标检测,这样的抽样方法是系统抽样;
②两个变量的线性相关程度越强,则相关系数的值越接近于1;
③两个分类变量X与Y的观测值κ2 , 若κ2越小,则说明“X与Y有关系”的把握程度越大;
④随机变量X~N(0,1),则P(|X|<1)=2P(X<1)﹣1.
A.①④
B.②④
C.①③
D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于的不等式![]() 的解集为
的解集为![]() ;
;
(1)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若存在两个不相等负实数![]() 、
、![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)是否存在实数![]() ,满足:“对于任意
,满足:“对于任意![]() ,都有
,都有![]() ,对于任意的
,对于任意的![]() ,都有
,都有![]() ”,若存在,求出
”,若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]()
(1)若不等式f(x)﹣f(x+m)≤1恒成立,求实数m的最大值;
(2)当a< ![]() 时,函数g(x)=f(x)+|2x﹣1|有零点,求实数a的取值范围.
时,函数g(x)=f(x)+|2x﹣1|有零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 某公司为了了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据 用户对其产品的满意度的评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频率分布表.A地区用户满意度评分的频率分布直方图
某公司为了了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据 用户对其产品的满意度的评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频率分布表.A地区用户满意度评分的频率分布直方图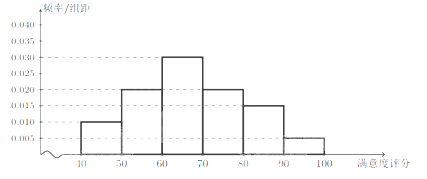
B地区用户满意度评分的频率分布表
满意度评分分组 | [50,60) | [50,60) | [50,60) | [50,60) | [50,60) |
频数 | 2 | 8 | 14 | 10 | 6 |
(1)(I)在答题卡上作出B地区用户满意度评分的频率分布直方图,并通过此图比较两地区满意度评分的平均值及分 散 程度.(不要求计算出具体值,给出结论即可)
B地区用户满意度评分的频率分布直方图
(2)(II)根据用户满意度评分,将用户的满意度评分分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
估计那个地区的用户的满意度等级为不满意的概率大,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 设a,b,c,d均为正数,且a+b=c+d,证明:(1)若ab > cd,则
设a,b,c,d均为正数,且a+b=c+d,证明:(1)若ab > cd,则 ![]() +
+![]() >
>![]() +
+ ![]() ;(2)
;(2) ![]() +
+![]() >
> ![]() +
+ ![]() 是|a-b| < |c-d|的充要条件
是|a-b| < |c-d|的充要条件
(1)(I)若ab![]() cd,则
cd,则![]() +
+![]()
![]()
![]() +
+![]()
(2)(II)![]() +
+![]()
![]()
![]() +
+![]() 是|a-b|
是|a-b|![]() |c-d|的充要条件
|c-d|的充要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015![]() 新课标II)已知椭圆C:9x2+y2=m2(m
新课标II)已知椭圆C:9x2+y2=m2(m![]() 0),直线l不过原点O且不平行于坐轴,l与C有两个交点A,B,线段AB的中点为M.
0),直线l不过原点O且不平行于坐轴,l与C有两个交点A,B,线段AB的中点为M.
(1)(I)证明:直线OM的斜率与l的斜率的乘积为定值;
(2)(II)若l过点(![]() ,m)延长线段OM与C交于点P,四边形OAPB能否为平行四边形?若能,求此时l的斜率,若不能,说明理由.
,m)延长线段OM与C交于点P,四边形OAPB能否为平行四边形?若能,求此时l的斜率,若不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)如图,椭圆E:![]() 的离心率是
的离心率是![]() ,过点P(0,1)的动直线l与椭圆相交于A,B两点,当直线l平行与x轴时,直线l被椭圆E截得的线段长为2
,过点P(0,1)的动直线l与椭圆相交于A,B两点,当直线l平行与x轴时,直线l被椭圆E截得的线段长为2![]() .
.
(1)求椭圆E的方程;
(2)在平面直角坐标系xOy中,是否存在与点P不同的定点Q,使得![]() 恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com