
【题目】下列说法正确的个数是( )
①某同学投篮的命中率为0.6,他10次投篮中命中的次数![]() 是一个随机变量,且
是一个随机变量,且![]() ;
;
②某福彩中奖概率为![]() ,某人一次买了8张,中奖张数
,某人一次买了8张,中奖张数![]() 是一个随机变量,且
是一个随机变量,且![]() ;
;
③从装有5个红球、5个白球的袋中,有放回地摸球,直到摸出白球为止,则摸球次数![]() 是随机变量,且
是随机变量,且![]()
A.0个B.1个C.2个D.3个
【答案】C
【解析】
利用独立重复试验的概念和二项分布的定义逐一分析判断每一个命题的真假即得解.
①某同学投篮的命中率为0.6,该同学投篮10次,是一个独立重复试验,所以他10次投篮中命中的次数![]() 是一个随机变量,且
是一个随机变量,且![]() ,所以该命题正确;
,所以该命题正确;
②某福彩中奖概率为![]() ,某人一次买了8张,相当于买了8次,每次中奖的概率都为
,某人一次买了8张,相当于买了8次,每次中奖的概率都为![]() ,相当于做了8次独立重复试验,中奖张数
,相当于做了8次独立重复试验,中奖张数![]() 是一个随机变量,且
是一个随机变量,且![]() ,所以该命题正确;
,所以该命题正确;
③从装有5个红球、5个白球的袋中,由于它是有放回地摸球,直到摸出白球为止,所以它不是一个独立重复性试验,因为当![]() 时,概率为
时,概率为![]() ,当
,当![]() 时,概率为
时,概率为![]() ,当
,当![]() 时,概率为
时,概率为![]() ,依次类推,即每次试验摸到白球的概率不相等,所以它不是独立重复性试验,所以
,依次类推,即每次试验摸到白球的概率不相等,所以它不是独立重复性试验,所以![]() 不服从
不服从![]() ,所以该命题错误.
,所以该命题错误.
故选:C


科目:高中数学 来源: 题型:
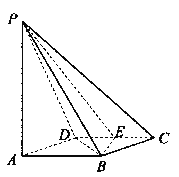
【题目】如图所示,四棱锥![]() 的底面
的底面![]() 是边长为1的菱形,
是边长为1的菱形,![]() ,
,
E是CD的中点,PA![]() 底面ABCD,
底面ABCD,![]() .
.
(I)证明:平面PBE![]() 平面PAB;
平面PAB;
(II)求二面角A—BE—P和的大小.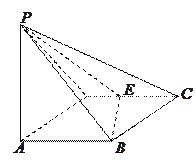
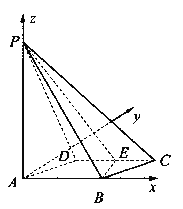
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利用一半径为4cm的圆形纸片(圆心为O)制作一个正四棱锥.方法如下:
(1)以O为圆心制作一个小的圆;
(2)在小的圆内制作一内接正方形ABCD;
(3)以正方形ABCD的各边向外作等腰三角形,使等腰三角形的顶点落在大圆上(如图);
(4)将正方形ABCD作为正四棱锥的底,四个等腰三角形作为正四棱锥的侧面折起,使四个等腰三角形的顶点重合,问:要使所制作的正四棱锥体积最大,则小圆的半径为

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)设数列![]() 的前
的前![]() 项和为
项和为![]() .已知
.已知![]() ,
, ![]() ,
, ![]() .
.
(1)写出![]() 的值,并求数列
的值,并求数列![]() 的通项公式;
的通项公式;
(2)记![]() 为数列
为数列![]() 的前
的前![]() 项和,求
项和,求![]() ;
;
(3)若数列![]() 满足
满足![]() ,
, ![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:

则下面结论中不正确的是
A. 新农村建设后,种植收入减少
B. 新农村建设后,其他收入增加了一倍以上
C. 新农村建设后,养殖收入增加了一倍
D. 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车驾驶学校在学员结业前,对学员的驾驶技术进行4次考核,规定:按顺序考核,一旦考核合格就不必参加以后的考核,否则还需参加下次考核。若学员小李独立参加每次考核合格的概率依次组成一个公差为![]() 的等差数列,他参加第一次考核合格的概率不超过
的等差数列,他参加第一次考核合格的概率不超过![]() ,且他直到参加第二次考核才合格的概率为
,且他直到参加第二次考核才合格的概率为![]() .
.
(1)求小李第一次参加考核就合格的概率![]() ;
;
(2)求小李参加考核的次数![]() 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图),

(1)由图中数据求a的值;
(2)若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为多少?
(3)估计这所小学的小学生身高的众数,中位数(保留两位小数)及平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y=f(x)的定义域为D,若对于任意x1,x2∈D,当x1+x2=2a时,恒有f(x1)+f(x2)=2b,则称点(a,b)为函数y=f(x)图象的对称中心.研究函数f(x)=x+sinπx﹣3的某一个对称中心,并利用对称中心的上述定义,可得到![]() 的值为( )
的值为( )
A.4035B.﹣4035C.8070D.﹣8070
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年10月28日,重庆公交车坠江事件震惊全国,也引发了广大群众的思考——如何做一个文明的乘客.全国各地大部分社区组织居民学习了文明乘车规范.![]() 社区委员会针对居民的学习结果进行了相关的问卷调查,并将得到的分数整理成如图所示的统计图.
社区委员会针对居民的学习结果进行了相关的问卷调查,并将得到的分数整理成如图所示的统计图.
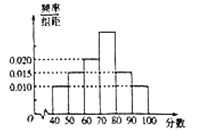
(1)求得分在![]() 上的频率;
上的频率;
(2)求![]() 社区居民问卷调查的平均得分的估计值;(同一组中的数据以这组数据所在区间中点的值作代表)
社区居民问卷调查的平均得分的估计值;(同一组中的数据以这组数据所在区间中点的值作代表)
(3)由于部分居民认为此项学习不具有必要性,![]() 社区委员会对社区居民的学习态度作调查,所得结果统计如下:(表中数据单位:人)
社区委员会对社区居民的学习态度作调查,所得结果统计如下:(表中数据单位:人)
认为此项学习十分必要 | 认为此项学习不必要 | |
50岁以上 | 400 | 600 |
50岁及50岁以下 | 800 | 200 |
根据上述数据,计算是否有![]() 的把握认为居民的学习态度与年龄相关.
的把握认为居民的学习态度与年龄相关.
附:![]() ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com