
【题目】如图,以棱长为1的正方体的具有公共顶点的三条棱所在直线为坐标轴,建立空间直角坐标系Oxyz,点P在对角线AB上运动,点Q在棱CD上运动.
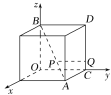
(1)当P是AB的中点,且2|CQ|=|QD|时,求|PQ|的值;
(2)当Q是棱CD的中点时,试求|PQ|的最小值及此时点P的坐标.
【答案】(1)![]() (2) 点P的坐标为(
(2) 点P的坐标为(![]() ), 最小值为
), 最小值为![]() .
.
【解析】
(1)根据正方体的性质可得![]() 的坐标,由两点间的距离公式计算可得结果;(2)根据题意,设点
的坐标,由两点间的距离公式计算可得结果;(2)根据题意,设点![]() 的横坐标为
的横坐标为![]() ,得
,得![]() =
=![]() .由
.由![]() ,可得
,可得![]() =
=![]() =
=![]() ,可得
,可得![]() 的坐标为
的坐标为![]() ,进而可以用
,进而可以用![]() 表示
表示![]() 的长,结合二次函数的性质分析可得结果.
的长,结合二次函数的性质分析可得结果.
(1)因为正方体的棱长为1,P是AB的中点,所以P(![]() ).
).
因为2|CQ|=|QD|,所以|CQ|=![]() ,所以Q(0,1,
,所以Q(0,1,![]() ).
).
由两点间的距离公式得:
|PQ|=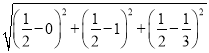 =
=![]() .
.
(2)如图,过点P作PE⊥OA于点E,则PE垂直于坐标平面xOy.
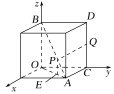
设点P的横坐标为x,则由正方体的性质可得点P的纵坐标也为x.
由正方体的棱长为1,得|AE|=![]() (1-x).
(1-x).
因为![]() ,
,
所以|PE|=![]() =1-x,
=1-x,
所以P(x,x,1-x).
又因为Q(0,1,![]() ),
),
所以|PQ|=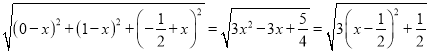
所以当x=![]() 时,|PQ|min=
时,|PQ|min=![]() ,即当点P的坐标为(
,即当点P的坐标为(![]() ),
),
即P为AB的中点时,|PQ|的值最小,最小值为![]() .
.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】十九大提出,坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村真脱贫,坚持扶贫同扶智相结合,帮助贫困村种植蜜柚,并利用电商进行销售,为了更好地销售,现从该村的蜜柚树上随机摘下了100个蜜柚进行测重,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 单位:克
单位:克![]() 中,其频率分布直方图如图所示.
中,其频率分布直方图如图所示.

![]() Ⅰ
Ⅰ![]() 按分层抽样的方法从质量落在
按分层抽样的方法从质量落在![]() ,
,![]() 的蜜柚中抽取5个,再从这5个蜜柚中随机抽取2个,求这2个蜜柚质量均小于2000克的概率;
的蜜柚中抽取5个,再从这5个蜜柚中随机抽取2个,求这2个蜜柚质量均小于2000克的概率;
![]() Ⅱ
Ⅱ![]() 以各组数据的中间数代表这组数据的平均水平,以频率代表概率,已知该贫困村的蜜柚树上大约还有5000个蜜柚等待出售,某电商提出两种收购方案:
以各组数据的中间数代表这组数据的平均水平,以频率代表概率,已知该贫困村的蜜柚树上大约还有5000个蜜柚等待出售,某电商提出两种收购方案:
A.所有蜜柚均以40元![]() 千克收购;
千克收购;
B.低于2250克的蜜柚以60元![]() 个收购,高于或等于2250克的以80元
个收购,高于或等于2250克的以80元![]() 个收购.
个收购.
请你通过计算为该村选择收益最好的方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a<2,函数f(x)=(x2+ax+a)ex.
(1)当a=1时,求f(x)的单调递增区间;
(2)若f(x)的极大值是6e-2,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() ⊥底面
⊥底面![]() ,底面
,底面![]() 为等边三角形,
为等边三角形,![]() ,
,![]() ,
, ![]() ,
,![]() 分别为
分别为![]() ,
, ![]() 的中点.
的中点.
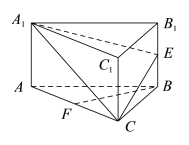
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成二面角的余弦值;
所成二面角的余弦值;
(3)设平面![]() 与平面
与平面![]() 的交线为
的交线为![]() 求证:
求证:![]() 与平面
与平面![]() 不平行.
不平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知等差数列{an}中,a1=1,a3=﹣3.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{an}的前k项和Sk=﹣35,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com