【题目】一件刚出土的珍贵文物要在博物馆大厅中央展出，需要设计各面是玻璃平面的无底正四棱柱将其罩住，罩内充满保护文物的无色气体.已知文物近似于塔形，高1.8米，体积0.5立方米，其底部是直径为0.9米的圆形，要求文物底部与玻璃罩底边至少间隔0.3米，文物顶部与玻璃罩上底面至少间隔0.2米，气体每立方米1000元，则气体费用最少为（ ）元
A.4500B.4000C.2880D.2380
灵星计算小达人系列答案
孟建平错题本系列答案科目：高中数学 来源： 题型：
【题目】某地区有800名学员参加交通法规考试,考试成绩的频率分布直方图如图所示,其中成绩分组区间是:
,
,
,
,
,规定90分及以上为合格:
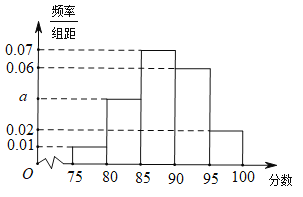
(1)求图中a的值;
(2)根据频率分布直方图估计该地区学员交通法规考试合格的概率;
(3)若三个人参加交通法规考试,估计这三个人至少有两人合格的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的离心率为
，焦距为
.斜率为k的直线l与椭圆M有两个不同的交点A，B.
（Ⅰ）求椭圆M的方程；
（Ⅱ）若
，求
的最大值；
（Ⅲ）设
，直线PA与椭圆M的另一个交点为C，直线PB与椭圆M的另一个交点为D.若C,D和点
共线，求k.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】函数
.
（1）求
的单调区间；
（2）在函数的图象上取
两个不同的点，令直线AB的斜率
为k，则在函数的图象上是否存在点
，且
，使得
？若存
在，求A，B两点的坐标，若不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】
11分制乒乓球比赛，每赢一球得1分，当某局打成10:10平后，每球交换发球权，先多得2分的一方获胜，该局比赛结束.甲、乙两位同学进行单打比赛，假设甲发球时甲得分的概率为0.5，乙发球时甲得分的概率为0.4，各球的结果相互独立.在某局双方10:10平后，甲先发球，两人又打了X个球该局比赛结束.
（1）求P（X=2）；
（2）求事件“X=4且甲获胜”的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列判断正确的是（ ）
A.若随机变量
服从正态分布
，
，则
；
B.已知直线
平面
，直线
平面
，则“
”是“
”的必要不充分条件；
C.若随机变量服从二项分布：
，则
；
D.已知直线
经过点
，则
的取值范围是
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某工厂产生的废气经过过滤后排放，规定排放时污染物的残留含量不得超过1%．已知在过滤过程中的污染物的残留数量P（单位：毫克/升）与过滤时间t（单位：小时）之间的函数关系为：
（
为正常数，
为原污染物数量）.若前5个小时废气中的污染物被过滤掉了90%，那么要能够按规定排放废气，至少还需要过滤（ ）
A. 
小时B. 
小时C. 5小时D. 
小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
