
【题目】如图,已知四棱锥的侧棱PD⊥底面ABCD,且底面ABCD是直角梯形,AD⊥CD,AB∥CD,AB=AD= ![]() CD=2,点M在侧棱上.
CD=2,点M在侧棱上.
(1)求证:BC⊥平面BDP;
(2)若侧棱PC与底面ABCD所成角的正切值为 ![]() ,点M为侧棱PC的中点,求异面直线BM与PA所成角的余弦值.
,点M为侧棱PC的中点,求异面直线BM与PA所成角的余弦值. 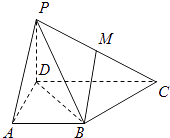
【答案】
(1)证明:由已知可算得 ![]() ,∴BD2+BC2=16=DC2,
,∴BD2+BC2=16=DC2,
故BD⊥BC,
又PD⊥平面ABCD,BC平面ABCD,故PD⊥BC,
又BD∩PD=D,所以BC⊥平面BDP
(2)解:如图,取PD中点为N,并连结AN,MN,BM∥AN,
则∠PAN即异面直线BM与PA所成角;
又PA⊥底面ABCD,∴∠PCD即为PC与底面ABCD所成角,
即 ![]() ,∴
,∴ ![]() ,即
,即 ![]() ,
,
又 ![]() ,
, ![]() ,则在△PAN中,
,则在△PAN中, ![]() =
= ![]() ,
,
即异面直线BM与PA所成角的余弦值为 ![]()
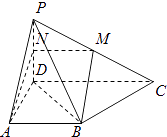
【解析】(1)证明BD⊥BC,PD⊥BC,即可证明BC⊥平面BDP;(2)取PD中点为N,并连结AN,MN,则∠PAN即异面直线BM与PA所成角,在△PAN中,利用余弦定理,即可求出异面直线BM与PA所成角的余弦值.
【考点精析】通过灵活运用异面直线及其所成的角和直线与平面垂直的判定,掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想即可以解答此题.


科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D. 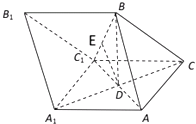
(1)求证:BD⊥A1C;
(2)若E在棱BC1上,且满足DE∥面ABC,求三棱锥E﹣ACC1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sinx的图象上所有点的横坐标缩小到原来的 ![]() (纵坐标不变),再将所得到的图象上所有点向左平移
(纵坐标不变),再将所得到的图象上所有点向左平移 ![]() 个单位,所得函数图象的解析式为( )
个单位,所得函数图象的解析式为( )
A.y=sin(2x﹣ ![]() )
)
B.y=sin(2x+ ![]() )
)
C.y=sin( ![]() x+
x+ ![]() )
)
D.y=sin( ![]() x+
x+ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以O为极点,x轴的正半轴为极轴的极坐标系中,直线l的极坐标方程为θ= ![]() ,曲线C的参数方程为
,曲线C的参数方程为 ![]() .
.
(1)写出直线l与曲线C的直角坐标方程;
(2)过点M平行于直线l1的直线与曲线C交于A、B两点,若|MA||MB|= ![]() ,求点M轨迹的直角坐标方程.
,求点M轨迹的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
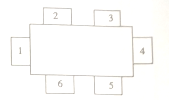
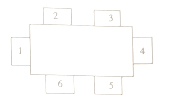
【题目】在一次体育兴趣小组的聚会中,要安排![]() 人的座位,使他们在如图所示的
人的座位,使他们在如图所示的![]() 个椅子中就坐,且相邻座位(如
个椅子中就坐,且相邻座位(如![]() 与
与![]() ,
, ![]() 与
与![]() )上的人要有共同的体育兴趣爱好.现已知这
)上的人要有共同的体育兴趣爱好.现已知这![]() 人的体育兴趣爱好如下表所示,且小林坐在
人的体育兴趣爱好如下表所示,且小林坐在![]() 号位置上,则
号位置上,则![]() 号位置上坐的是( )
号位置上坐的是( )
小林 | 小方 | 小马 | 小张 | 小李 | 小周 | |
体育兴趣爱好 | 篮球,网球,羽毛球 | 足球,排球,跆拳道 | 篮球,棒球,乒乓球 | 击剑,网球,足球 | 棒球,排球,羽毛球 | 跆拳道,击剑,自行车 |
A. 小方 B. 小张 C. 小周 D. 小马
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知二面角α﹣MN﹣β的大小为60°,菱形ABCD在面β内,A、B两点在棱MN上,∠BAD=60°,E是AB的中点,DO⊥面α,垂足为O. 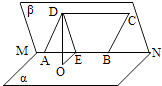
(1)证明:AB⊥平面ODE;
(2)求异面直线BC与OD所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com