
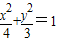 的实线上运动,若AB∥x轴,点N的坐标为(1,0),则△ABN的周长l的取值范围是 .
的实线上运动,若AB∥x轴,点N的坐标为(1,0),则△ABN的周长l的取值范围是 .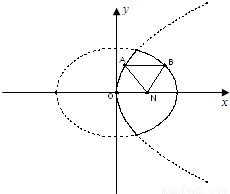
 =
=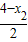 ,进而表示出三角形周长,化简整理后,求得周长L关于x2的表达式,联立抛物线和椭圆方程求得两曲线的交点,判断出x2的范围,进而确定L的范围.
,进而表示出三角形周长,化简整理后,求得周长L关于x2的表达式,联立抛物线和椭圆方程求得两曲线的交点,判断出x2的范围,进而确定L的范围. =
=
 =
=
 或-6(舍负)
或-6(舍负) ≤x2≤2
≤x2≤2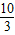 ≤
≤ ≤4
≤4 )
) =1,x=1,或 x=-
=1,x=1,或 x=- (舍去),
(舍去),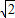 ,
, ,
, ),
),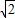


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
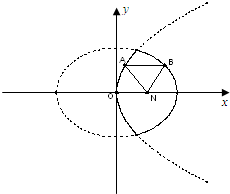 [理]如图,已知动点A,B分别在图中抛物线y2=4x及椭圆
[理]如图,已知动点A,B分别在图中抛物线y2=4x及椭圆| x2 |
| 4 |
| y2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
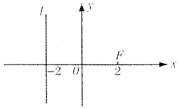
(08年滨州市质检三理) 如图,已知点F(2,0),直线![]() 为该平面上的动点,过P做直线l的垂直,垂足为Q,且
为该平面上的动点,过P做直线l的垂直,垂足为Q,且![]()
(1)求动点P的轨迹C的方程;
(2)设过A(-2,0)的直线m交轨迹C于M,N两点,且∠MFN为锐角,求直线m的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(05年浙江卷理)(14分)
如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|∶|A1F1|=2∶1.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线l1:x=m(|m|>1),P为l1上的动点,使∠F1PF2最大的点P记为Q,求点Q的坐标(用m表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com