
【题目】已知函数![]()
(1)若![]() ,求
,求![]() 的极值;
的极值;
(2)若![]() ,都有
,都有![]() 成立,求k的取值范围.
成立,求k的取值范围.
科目:高中数学 来源: 题型:
【题目】某工厂打算设计一种容积为2m3的密闭容器用于贮藏原料,容器的形状是如图所示的直四棱柱,其底面是边长为x米的正方形,假设该容器的底面及侧壁的厚度均可忽略不计.
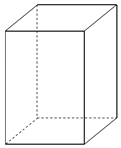
(1)请你确定x的值,使得该容器的外表面积最小;
(2)若该容器全部由某种每平方米价格为100元的材料做成,且制作该容器仅需将购置的材料做成符合需要的矩形,这些矩形即是直四棱柱形容器的上下底面和侧面(假设这一过程中产生的费用和材料损耗可忽略不计),再将这些上下底面和侧面的边缘进行焊接即可做成该容器,焊接费用是每米500元,试确定x的值,使得生产每个该种容器的成本(即原料购置成本+焊接费用)最低.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型歌手选秀活动,过程分为初赛、复赛和决赛.经初赛进入复赛的40名选手被平均分成甲、乙两个班,由组委会聘请两位导师各负责一个班进行声乐培训.下图是根据这40名选手参加复赛时获得的100名大众评审的支持票数制成的茎叶图.赛制规定:参加复赛的40名选手中,获得的支持票数不低于85票的可进入决赛,其中票数不低于95票的选手在决赛时拥有“优先挑战权”.
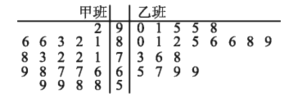
(1)从进入决赛的选手中随机抽出2名,X表示其中拥有“优先挑战权”的人数,求X的分布列和数学期望;
(2)请填写下面的![]() 列联表,并判断能否在犯错误的概率不超过0.025的前提下认为进入决赛与选择的导师有关?
列联表,并判断能否在犯错误的概率不超过0.025的前提下认为进入决赛与选择的导师有关?
甲班 | 乙班 | 合计 | |
进入决赛 | |||
未进入决赛 | |||
合计 |
下面的临界值表仅供参考:
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: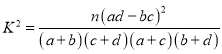 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示,在等腰梯形ABCD中,![]() ,
,![]() ,垂足为E,
,垂足为E,![]() ,
,![]() 将
将![]() 沿EC折起到
沿EC折起到![]() 的位置,如图2所示,使平面
的位置,如图2所示,使平面![]() 平面ABCE.
平面ABCE.
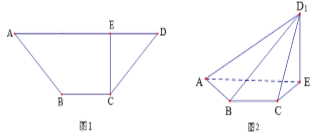
(1)连结BE,证明:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在点G,使得
上是否存在点G,使得![]() 平面
平面![]() ,若存在,直接指出点G的位置
,若存在,直接指出点G的位置![]() 不必说明理由
不必说明理由![]() ,并求出此时三棱锥
,并求出此时三棱锥![]() 的体积;若不存在,请说明理由.
的体积;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣2mx﹣n(0<x<1),其中m,n∈R,e为自然对数的底数.
(1)试讨论函数f(x)的极值;
(2)记函数g(x)=ex﹣mx2﹣nx﹣1(0<x<1),且g(x)的图象在点![]() 处的切的斜率为
处的切的斜率为![]() ,若函数g(x)存在零点,试求实数m的取值范围.
,若函数g(x)存在零点,试求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com