
分析 运用a1=S1,n>1时,sn-sn-1=an,用作差法得到an,an-1的关系,再由等差数列的定义和通项公式可得,an=(n+1)•2n,再求得Sn=n•2n+1,再对n讨论为偶数和奇数,运用数列的单调性,解不等式即可得到所求范围.
解答 解:当n=1时,S1=2a1-22得a1=4.
Sn=2an-2n+1,
当n≥2时,Sn-1=2an-1-2n,
两式相减得an=2an-2an-1-2n即an=2an-1+2n,
所以$\frac{{a}_{n}}{{2}^{n}}$=$\frac{{a}_{n-1}}{{2}^{n-1}}$+1
又$\frac{{a}_{1}}{{2}^{1}}$=2,
所以数列{$\frac{{a}_{n}}{{2}^{n}}$}是以2为首项,1为公差的等差数列.
$\frac{{a}_{n}}{{2}^{n}}$=2+n-1,即an=(n+1)•2n,
Sn=2(n+1)•2n-2n+1=n•2n+1,
即有$\frac{{S}_{n}}{{S}_{n+1}}$=$\frac{n•{2}^{n+1}}{(n+1)•{2}^{n+2}}$=$\frac{n}{2(n+1)}$,
当n为偶数时,(-1)nλ<$\frac{{S}_{n}}{{S}_{n+1}}$,即为λ<$\frac{n}{2(n+1)}$的最小值,
由$\frac{n}{2(n+1)}$=$\frac{1}{2(1+\frac{1}{n})}$递增,可得n=2时,取得最小值$\frac{1}{3}$,
则λ<$\frac{1}{3}$;
当n为奇数时,即有-λ<$\frac{n}{2(n+1)}$的最小值,
由n=1时,取得最小值,且为$\frac{1}{4}$,
解得λ>-$\frac{1}{4}$,
综上可得,λ的范围是(-$\frac{1}{4}$,$\frac{1}{3}$).
故答案为:(-$\frac{1}{4}$,$\frac{1}{3}$).
点评 本题考查了通项公式与前n项和公式的关系,等差数列的定义的应用.恒成立问题主要利用分离参数法转化为求最值问题解决.


科目:高中数学 来源: 题型:选择题
| A. | a${\;}^{-\frac{1}{2}}$•a${\;}^{\frac{1}{2}}$=0 | B. | a${\;}^{\frac{1}{2}}$÷a${\;}^{\frac{1}{3}}$=a${\;}^{\frac{5}{6}}$ | ||
| C. | (a3)2=a9 | D. | a${\;}^{\frac{1}{2}}$•a${\;}^{\frac{1}{2}}$=a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,6} | B. | {1,5} | C. | {1,6} | D. | {5,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
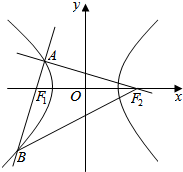 如图,过双曲线上左支一点A作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点B,若($\overrightarrow{AB}$+$\overrightarrow{A{F}_{2}}$)•$\overrightarrow{B{F}_{2}}$=0,则双曲线的离心率为( )
如图,过双曲线上左支一点A作两条相互垂直的直线分别过两焦点,其中一条与双曲线交于点B,若($\overrightarrow{AB}$+$\overrightarrow{A{F}_{2}}$)•$\overrightarrow{B{F}_{2}}$=0,则双曲线的离心率为( )| A. | $\sqrt{5+2\sqrt{2}}$ | B. | $\sqrt{5-2\sqrt{2}}$ | C. | $\sqrt{4+2\sqrt{2}}$ | D. | $\sqrt{4-2\sqrt{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com