
【题目】已知椭圆![]() 的短轴长为2,离心率
的短轴长为2,离心率![]() ,
,
(1)求椭圆![]() 方程;
方程;
(2)若直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,与圆
,与圆![]() 相切于点
相切于点![]() ,
,
①证明:![]() (其中
(其中![]() 为坐标原点);
为坐标原点);
②设![]() ,求实数
,求实数![]() 的取值范围..
的取值范围..
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源: 题型:
【题目】唐代诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题一“将军饮马”问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为![]() ,若将军从点
,若将军从点![]() 处出发,河岸线所在直线方程为
处出发,河岸线所在直线方程为![]() ,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( ).
,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年10月1日是新中国的第70个国庆日,庄重的阅兵、欢乐的游行、热烈的联欢尽显祖国的繁荣昌盛.为了了解当天某校900名高三学生的观看情况,从中抽取了100名学生,情况如下表所示:
观看情况 | 电视观看 | 网络观看 | 没有观看 |
人数 | 35 | 60 | 5 |
新时代下,网络观看使用最多的是手机,其它还有电脑、ipad等.“是否使用手机观看”与“学生的性别”之间对应的列联表如下:
使用手机观看 | 其它方式观看 | 合计 | |
男学生 | 20 | 8 | 28 |
女学生 | 20 | 12 | 32 |
合计 | 40 | 20 | 60 |
(1)估计该校高三学生当天的观看人数.
(2)当天没有观看的5名学生中,有3人第二天观看了重播.从这5名学生中任选2人求这2人第二天都看了重播的概率;
(3)根据列联表判断,能否有95%的把握认为网络观看的学生中“是否使用手机观看”与“学生的性别”有关?
附: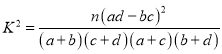 ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 九章算术
九章算术![]() 是我国古代著名数学经典
是我国古代著名数学经典![]() 其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小
其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小![]() 以锯锯之,深一寸,锯道长一尺
以锯锯之,深一寸,锯道长一尺![]() 问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺
问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺![]() 问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示
问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示![]() 阴影部分为镶嵌在墙体内的部分
阴影部分为镶嵌在墙体内的部分![]() 已知弦
已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算该木材镶嵌在墙中的体积约为( )(注:1丈
寸,估算该木材镶嵌在墙中的体积约为( )(注:1丈![]() 尺
尺![]() 寸,
寸,![]() ,
,![]() )
)

A. 600立方寸 B. 610立方寸 C. 620立方寸 D. 633立方寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年暑假期间,河南有一新开发的景区在各大媒体循环播放广告,观众甲首次看到该景区的广告后,不来此景区的概率为![]() ,从第二次看到广告起,若前一次不来此景区,则这次来此景区的概率是
,从第二次看到广告起,若前一次不来此景区,则这次来此景区的概率是![]() ,若前一次来此景区,则这次来此景区的概率是
,若前一次来此景区,则这次来此景区的概率是![]() .记观众甲第n次看到广告后不来此景区的概率为
.记观众甲第n次看到广告后不来此景区的概率为![]() ,若当
,若当![]() 时,
时,![]() 恒成立,则M的最小值为__________.
恒成立,则M的最小值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
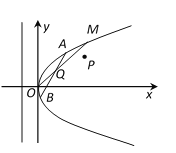
【题目】如图所示,在直角坐标系![]() 中,点
中,点![]() 到抛物线
到抛物线![]() 的准线的距离为
的准线的距离为![]() ,点
,点![]() 是
是![]() 上的定点,
上的定点,![]() 、
、![]() 是
是![]() 上的两个动点,且线段
上的两个动点,且线段![]() 的中点
的中点![]() 在线段
在线段![]() 上.
上.
(1)抛物线![]() 的方程及
的方程及![]() 的值;
的值;
(2)当点![]() 、
、![]() 分别在第一、四象限时,求
分别在第一、四象限时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列![]() 首项和公差都是
首项和公差都是![]() ,记
,记![]() 的前n项和为
的前n项和为![]() ,等比数列
,等比数列![]() 各项均为正数,公比为q,记
各项均为正数,公比为q,记![]() 的前n项和为
的前n项和为![]() :
:
(1)写出![]()
![]() 构成的集合A;
构成的集合A;
(2)若将![]() 中的整数项按从小到大的顺序构成数列
中的整数项按从小到大的顺序构成数列![]() ,求
,求![]() 的一个通项公式;
的一个通项公式;
(3)若q为正整数,问是否存在大于1的正整数k,使得![]()
![]() 同时为(1)中集合A的元素?若存在,写出所有符合条件的
同时为(1)中集合A的元素?若存在,写出所有符合条件的![]() 的通项公式,若不存在,请说明理由.
的通项公式,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com