
【题目】我国古代数学名著《九章算术商功》中阐述:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”若称为“阳马”的某几何体的三视图如图所示,图中网格纸上小正方形的边长为1,对该几何体有如下描述:
①四个侧面都是直角三角形;
②最长的侧棱长为![]() ;
;
③四个侧面中有三个侧面是全等的直角三角形;
④外接球的表面积为24π.
其中正确的描述为____.

科目:高中数学 来源: 题型:
【题目】已知椭圆与抛物线y2=![]() x有一个相同的焦点,且该椭圆的离心率为
x有一个相同的焦点,且该椭圆的离心率为![]() .
.
(1)求椭圆的标准方程;
(2)过点P(0,1)的直线与该椭圆交于A,B两点,O为坐标原点,若![]() ,求△AOB的面积.
,求△AOB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电量最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为5000万元;若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某幼儿园举办“yue”主题系列活动——“悦”动越健康亲子运动打卡活动,为了解小朋友坚持打卡的情况,对该幼儿园所有小朋友进行了调查,调查结果如下表:
打卡天数 | 17 | 18 | 19 | 20 | 21 |
男生人数 | 3 | 5 | 3 | 7 | 2 |
女生人数 | 3 | 5 | 5 | 7 | 3 |
(1)根据上表数据,求该幼儿园男生平均打卡的天数;
(2)若从打卡21天的小朋友中任选2人交流心得,求选到男生和女生各1人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 满足
满足![]() ,
,![]() ,
,![]() 为非零常数.
为非零常数.
(1)是否存在实数![]() ,使得数列
,使得数列![]() 成为等差数列或等比数列,若存在,找出所有的
成为等差数列或等比数列,若存在,找出所有的![]() ,及对应的通项公式;若不存在,说明理由;
,及对应的通项公式;若不存在,说明理由;
(2)当![]() 时,记
时,记![]() ,证明:数列
,证明:数列![]() 是等比数列;
是等比数列;
(3)求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体ABCD-A1B1C1D1 的棱长为 2,且AC 与BD 交于点O,E 为棱DD1 中点,以A 为原点,建立空间直角坐标系A-xyz,如图所示.
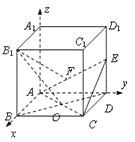
(Ⅰ)求证:B1O⊥平面EAC;
(Ⅱ)若点F 在EA 上且B1F⊥AE,试求点F 的坐标;
(Ⅲ)求二面角B1-EA-C 的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() .
.
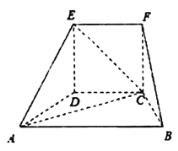
(1)求证:![]() 平面FBC;
平面FBC;
(2)线段ED上是否存在点Q,使平面![]() 平面QBC?证明你的结论.
平面QBC?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农户计划种植莴笋和西红柿,种植面积不超过![]() 亩,投入资金不超过
亩,投入资金不超过![]() 万元,假设种植莴笋和西红柿的产量、成本和售价如下表:
万元,假设种植莴笋和西红柿的产量、成本和售价如下表:
年产量/亩 | 年种植成本/亩 | 每吨售价 | |
莴笋 | 5吨 | 1万元 | 0.5万元 |
西红柿 | 4.5吨 | 0.5万元 | 0.4万元 |
那么,该农户一年种植总利润(总利润=总销售收入-总种植成本)的最大值为____万元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com