
【题目】已知椭圆的中心在原点,焦点为 ![]() ,且离心率
,且离心率 ![]() .
.
(1)求椭圆的方程;
(2)求以点P(2,﹣1)为中点的弦所在的直线方程.
【答案】
(1)解:∵椭圆的中心在原点,焦点为 ![]() ,且离心率
,且离心率 ![]() ,
,
∴  ,解得a=4,c=2
,解得a=4,c=2 ![]() ,b=2,
,b=2,
∴椭圆方程为 ![]()
(2)解:设以点P(2,﹣1)为中点的弦与椭圆交于点A(x1,y1),B(x2,y2),
则x1+x2=4,y1+y2=﹣2,
∴ ![]() ,两式相减,并整理,得4(x1﹣x2)﹣8(y1﹣y2)=0,
,两式相减,并整理,得4(x1﹣x2)﹣8(y1﹣y2)=0,
∴k= ![]() =
= ![]() ,
,
∴以点P(2,﹣1)为中点的弦所在的直线方程为:
y+1= ![]() (x﹣2),即x﹣2y﹣4=0
(x﹣2),即x﹣2y﹣4=0
【解析】(1)由椭圆的焦点和离心率列出方程组,求出a,b,由此能求出椭圆方程.(2)设以点P(2,﹣1)为中点的弦与椭圆交于点A(x1 , y1),B(x2 , y2),则x1+x2=4,y1+y2=﹣2,由此利用点差法能求出以点P(2,﹣1)为中点的弦所在的直线方程.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源: 题型:
【题目】要得到函数y=cos(2x﹣ ![]() )的图象,只需将函数y=sin2x的图象( )
)的图象,只需将函数y=sin2x的图象( )
A.向左平移 ![]() 个单位
个单位
B.向左平移 ![]() 个单位
个单位
C.向右平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,侧面ABC是一个等腰直角三角形,∠BAC=90°,底面BCD是一个等边三角形,平面ABC⊥平面BCD,E为BD的中点,则AE与平面BCD所成角的大小为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形草坪AMPN中,点C在对角线MN上.CD垂直于AN于点D,CB垂直于AM于点B,|CD|=|AB|=3米,|AD|=|BC|=2米,设|DN|=x米,|BM|=y米.求这块矩形草坪AMPN面积的最小值. 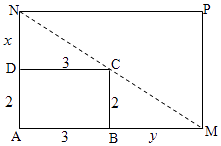
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,已知AA1=AB=AC,BC= ![]() AB,且AA1⊥平面ABC,点M、Q分别是BC、CC1的中点,点P是棱A1B1上的任一点.
AB,且AA1⊥平面ABC,点M、Q分别是BC、CC1的中点,点P是棱A1B1上的任一点. 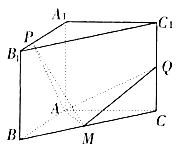
(1)求证:AQ⊥MP;
(2)若平面ACC1A1与平面AMP所成的锐角二面角为θ,且cosθ= ![]() ,试确定点P在棱A1B1上的位置,并说明理由.
,试确定点P在棱A1B1上的位置,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() (a>0,b>0)上的点P到左、右两焦点F1 , F2的距离之和为2
(a>0,b>0)上的点P到左、右两焦点F1 , F2的距离之和为2 ![]() ,离心率为
,离心率为 ![]() .
.
(1)求椭圆的方程;
(2)是否存在同时满足①②两个条件的直线l?
①过点M(0, ![]() );
);
②存在椭圆上与右焦点F2共线的两点A、B,且A、B关于直线l对称.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,E为棱SC的中点,若AC=2 ![]() ,SA=SB=AB=BC=SC=2,则异面直线AC与BE所成的角为( )
,SA=SB=AB=BC=SC=2,则异面直线AC与BE所成的角为( ) 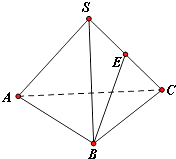
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com