【答案】
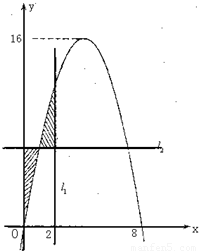
分析:(Ⅰ)由图象可知函数图象过点(0,0),(8,0),并且f(x)的最大值为16,分别代入即可解得a、b、c的值
(Ⅱ)先求出直线l
1:y=-t
2+8t(其中0≤t≤2.t为常数)与抛物线f(x)=-x
2+8x的交点横坐标(用t表示),再利用定积分的几何意义求两部分面积之和即可
(Ⅲ)先令H(x)=g(x)-f(x)=x
2-8x+6lnx+m,要使函数f(x)与函数g(x)有且仅有2个不同的交点,则函数H(x)=x
2-8x+6lnx+m的图象与x轴的正半轴有且只有两个不同的交点,再利用导数研究函数H(x)的单调性和极值,数形结合得满足题意的不等式组,解之可得m的值
解答:解:(I)由图形可知二次函数的图象过点(0,0),(8,0),并且f(x)的最大值为16
则

,
∴函数f(x)的解析式为f(x)=-x
2+8x
(Ⅱ)由
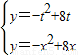
得x
2-8x-t(t-8)=0,∴x
1=t,x
2=8-t,
∵0≤t≤2,∴直线l
1与f(x)的图象的交点坐标为(t,-t
2+8t)
由定积分的几何意义知:
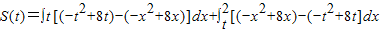
=
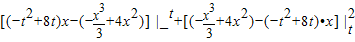
=
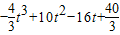
(Ⅲ)令H(x)=g(x)-f(x)=x
2-8x+6lnx+m.
因为x>0,要使函数f(x)与函数g(x)有且仅有2个不同的交点,则函数H(x)=x
2-8x+6lnx+m的图象与x轴的正半轴有且只有两个不同的交点
∴
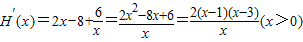
∴x=1或x=3时,H′(x)=0
当x∈(0,1)时,H′(x)>0,H(x)是增函数;
当x∈(1,3)时,H′(x)<0,H(x)是减函数
当x∈(3,+∞)时,H′(x)>0,H(x)是增函数
∴H(x)极大值为H(1)=m-7;H(x)极小值为H(3)=m+6ln3-15
又因为当x→0时,H(x)→-∞;当x→+∞时,H(x)→+∞
所以要使ϕ(x)=0有且仅有两个不同的正根,必须且只须
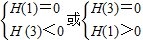
即
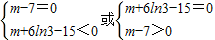
,∴m=7或m=15-6ln3.
∴当m=7或m=15-6ln3.时,函数f(x)与g(x)的图象有且只有两个不同交点
点评:本题综合考查了二次函数的图象和性质、定积分的几何意义、导数与函数零点等多个知识点,解题时要综合掌握各种知识,熟练运用数形结合、分类讨论思想解决问题

 ,
,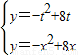 得x2-8x-t(t-8)=0,∴x1=t,x2=8-t,
得x2-8x-t(t-8)=0,∴x1=t,x2=8-t,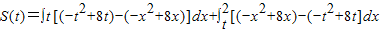 =
=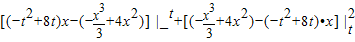 =
=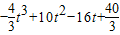
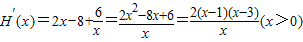
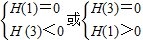
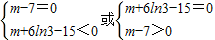 ,∴m=7或m=15-6ln3.
,∴m=7或m=15-6ln3.
