
【题目】已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN= ![]() .
.
(Ⅰ)求证:BD⊥PC;
(Ⅱ)求证:MN∥平面PDC;
(Ⅲ)求二面角A﹣PC﹣B的余弦值.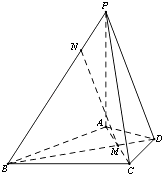
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={x|﹣2<x<2},N={x|x2﹣2x﹣3<0},则集合M∩N=( )
A.{x|x<﹣2}
B.{x|x>3}
C.{x|﹣1<x<2}
D.{x|2<x<3}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是某县参加2007年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为A1 , A2 , …,A10(如A2表示身高(单位:cm)在[150,155)内的学生人数)图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~180cm(含160cm,不含180cm)的学生人数,那么在流程图中的判断框内应填写的条件是( ) 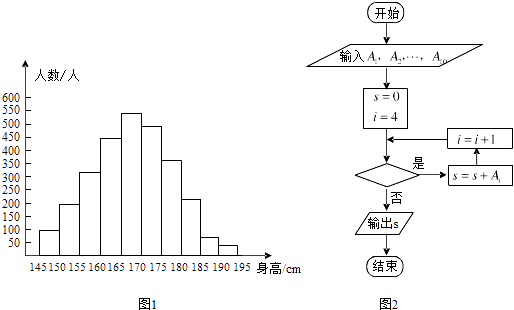
A.i<6
B.i<7
C.i<8
D.i<9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+|x﹣a|+1,x∈R,a∈R.
(Ⅰ)当a=1时,求函数f(x)的最小值;
(Ⅱ)若函数f(x)的最小值为g(a),令m=g(a),求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1的底面ABCD是平行四边形,且AB=1,BC=2,∠ABC=60°,E为BC的中点,AA1⊥平面ABCD. (Ⅰ)证明:平面A1AE⊥平面A1DE;
(Ⅱ)若DE=A1E,试求二面角E﹣A1C﹣D的余弦值.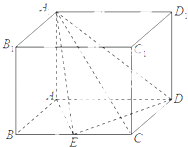
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com