
【题目】已知关于![]() 的方程为
的方程为![]() .
.
(Ⅰ)若![]() ,
,![]() ,求方程有实数根的概率.
,求方程有实数根的概率.
(Ⅱ)若![]() ,
,![]() ,求方程有实数根的概率.
,求方程有实数根的概率.
(Ⅲ)在区间![]() 上任取两个数
上任取两个数![]() 和
和![]() ,利用随机数模拟的方法近似计算关于
,利用随机数模拟的方法近似计算关于![]() 的方程
的方程![]() 有实数根的概率,请写出你的试验方法.
有实数根的概率,请写出你的试验方法.
【答案】(I)![]() ;(II)
;(II)![]() ;(III)试验方法见解析.
;(III)试验方法见解析.
【解析】
试题分析:(I)由方程有根解出![]() 的范围,端点值之差的绝对值即长度之比即为所求;(II)由方程有根得出
的范围,端点值之差的绝对值即长度之比即为所求;(II)由方程有根得出![]() 的不等式组,在平面直角坐标系中画出图形的可行域,面积之比即为所求;(III)试验的总次数之比即为所求的概率值.
的不等式组,在平面直角坐标系中画出图形的可行域,面积之比即为所求;(III)试验的总次数之比即为所求的概率值.
试题解析:解:(Ⅰ)方程![]() 有实数根等价于
有实数根等价于![]() 即
即![]() , ……1分
, ……1分
由几何概型概率公式得方程有解的概率为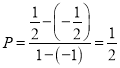 . …………3分
. …………3分
(Ⅱ)方程![]() 有实数根等价于
有实数根等价于![]() .
.![]() 或
或![]() .
.
…………4分
![]() 可看成是平面内的点,试验的所有结果所构成的区域为
可看成是平面内的点,试验的所有结果所构成的区域为![]() ,
,
这是一个正方形区域,面积为![]() , …………6分
, …………6分
设事件![]() ,则
,则![]() 构成的区域为
构成的区域为
![]()
面积为![]() , …………8分
, …………8分
所以由几何概性概率告诉的关于![]() 的方程
的方程![]() 有实数根的概率
有实数根的概率![]() .
.
…………9分
(Ⅲ)第一步:利用计算器或者计算机产生两组0到1之间的随机数:![]() ,
,![]() ;
;
第二步:统计试验的总次数![]() ”的次数
”的次数![]() ;
;
第三步:计算频率![]() ,得出概率的近似值为
,得出概率的近似值为![]() . …………12分
. …………12分


科目:高中数学 来源: 题型:
【题目】(多选)下列调查中,适宜采用抽样调查的是( )
A.调查某市中小学生每天的运动时间
B.某幼儿园中有位小朋友得了手足口病,对此幼儿园中的小朋友进行检查
C.农业科技人员调查今年麦穗的单穗平均质量
D.调查某快餐店中8位店员的生活质量情况
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校将5个参加知识竞赛的名额全部分配给高二年级的4个班级,其中甲班级至少分配2个名额,其它班级可以不分配名额或分配多个名额,则不同的分配方案共有( )
A.30种 B.26种 C.24种 D.20种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农场预算用5600元购买单价为50元(每吨)的钾肥和20元(每吨)的氮肥,希望使两种肥料的总数量(吨)尽可能的多,但氮肥数不少于钾肥数,且不多于钾肥数的1.5倍
(Ⅰ)设买钾肥![]() 吨,买氮肥
吨,买氮肥![]() 吨,按题意列出约束条件、画出可行域,并求钾肥、氮肥各买多少才行?
吨,按题意列出约束条件、画出可行域,并求钾肥、氮肥各买多少才行?
(Ⅱ)已知![]() ,
,![]() 是坐标原点,
是坐标原点, ![]() 在(Ⅰ)中的可行域内,求
在(Ⅰ)中的可行域内,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对一批电子元件进行寿命追踪调查,从这批产品中抽取![]() 个产品(其中
个产品(其中![]() ),得到频率分布直方图如下:
),得到频率分布直方图如下:

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)从频率分布直方图估算这批电子元件寿命的平均数、中位数的估计分别是多少?
(Ⅲ)现要从300![]() 400及400
400及400![]() 500这两组中按照分层抽样的方法抽取一个样本容量为36的样本,则在300
500这两组中按照分层抽样的方法抽取一个样本容量为36的样本,则在300![]() 400及400
400及400![]() 500这两组分别抽多少件产品.
500这两组分别抽多少件产品.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某班学生的身高情况,决定从50名学生(已编号为00~49)中选取10名进行测量,利用随机数法进行抽取,得到如下4组编号,则正确的编号是( )
A.26,94,29,27,43,99,55,19,81,06B.20,26,31,40,24,36,19,34,03,48
C.02,38,22,41,38,24,49,44,03,11D.04,00,45,32,44,22,04,11,08,49
查看答案和解析>>
科目:高中数学 来源: 题型:
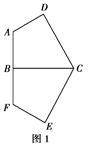
【题目】已知平面五边形![]() 是轴对称图形(如图1),BC为对称轴,AD⊥CD,AD=AB=1,
是轴对称图形(如图1),BC为对称轴,AD⊥CD,AD=AB=1,![]() ,将此五边形沿BC折叠,使平面ABCD⊥平面BCEF,得到如图2所示的空间图形,对此空间图形解答下列问题.
,将此五边形沿BC折叠,使平面ABCD⊥平面BCEF,得到如图2所示的空间图形,对此空间图形解答下列问题.
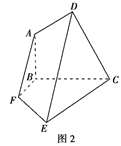
(1)证明:AF∥平面DEC;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在整数集![]() 中,被4除所得余数为
中,被4除所得余数为![]() 的所有整数组成一个“类”,记为
的所有整数组成一个“类”,记为![]() ,则下列结论正确的为 .
,则下列结论正确的为 .
①2014![]() ;
;
②-1![]() ;
;
③![]() ;
;
④命题“整数![]() 满足
满足![]() ,则
,则![]() ”的原命题与逆命题都正确;
”的原命题与逆命题都正确;
⑤“整数![]() 属于同一类”的充要条件是“
属于同一类”的充要条件是“![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①函数![]() 的图像过定点
的图像过定点![]() ;
;
②已知函数![]() 是定义在
是定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
时,![]() ,则
,则![]() 的解析式为
的解析式为![]() ;
;
③函数![]() 的图像可由函数
的图像可由函数![]() 图像向右平移一个单位得到;
图像向右平移一个单位得到;
④函数![]() 图像上的点到
图像上的点到![]() 距离的最小值是
距离的最小值是![]() .
.
其中所有正确命题的序号是_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com