
改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村2001到2005年五年间每年考入大学的人数,为了方便计算,2001年编号为1,2002年编号为2,……,2005年编号为5,数据如下:
| 年份(x) | 1 | 2 | 3 | 4 | 5 |
| 人数(y) | 3 | 5 | 8 | 11 | 13 |
 年多于10人的概率.
年多于10人的概率.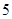 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出 关于
关于 的回归方程
的回归方程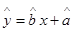 ,并计算第
,并计算第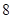 年的估计值。
年的估计值。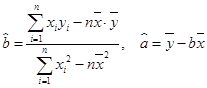
(1) ;(2)
;(2) .
.
解析试题分析:.(1)从这5年中任意抽取两年,共有10种抽取方法,至少有一年多于10人的事件有7种,利用古典概型的概率计算公式直接求出其概率;(2)由给出的数据,利用最小二乘法求线性回归方程系数公式求出系数,从而得到线性回归方程,再利用回归方程估计第8年的估计值.
试题解析:(1)从这5年中任意抽取两年,所有的事件有:12,13,14,15,23,24,25,34,35,45共10种,至少有1年多于10人的事件有:14, 15,24,25,34,45,45共7种,则至少有1年多于10人的概率为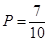 .
.
(2)由已知数据得
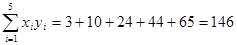 ,
,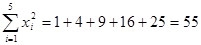 ,
,
则
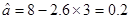 ,则回归直线的方程为:
,则回归直线的方程为: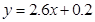
则第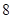 年的估计值为
年的估计值为 .
.
考点:本题考查了古典概型的概率公式,线性回归方程的求解和线性回归分析.


科目:高中数学 来源: 题型:解答题
为了让学生了解更多“奥运会”知识,某中学举行了一次“奥运知识竞赛”,共有800名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表,解答下列问题:
| 分组 | 频数 | 频率 |
| 60.5~70.5 | | 0.16 |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | 18 | 0.36 |
| 90.5~100.5 | | |
| 合计 | 50 | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.
(1)计算甲班的样本方差;
(2)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量 (简称血酒含量,单位是毫克/
(简称血酒含量,单位是毫克/ 毫升),当
毫升),当 时,为“酒后驾车”;当
时,为“酒后驾车”;当 时,为“醉酒驾车”.某市公安局交通管理部门于
时,为“醉酒驾车”.某市公安局交通管理部门于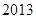 年
年 月的某天晚上
月的某天晚上 点至
点至 点在该市区解放路某处设点进行一次拦查行动,共依法查出了
点在该市区解放路某处设点进行一次拦查行动,共依法查出了 名饮酒后违法驾驶机动车者,如图为这
名饮酒后违法驾驶机动车者,如图为这 名驾驶员抽血检测后所得结果画出的频率分布直方图(其中
名驾驶员抽血检测后所得结果画出的频率分布直方图(其中 的人数计入
的人数计入 人数之内).
人数之内).
(Ⅰ)求此次拦查中“醉酒驾车”的人数;
(Ⅱ)从违法驾车的 人中按“酒后驾车”和“醉酒驾车”利用分层抽样抽取
人中按“酒后驾车”和“醉酒驾车”利用分层抽样抽取 人做样本进行研究,再从抽取的
人做样本进行研究,再从抽取的 人中任取
人中任取 人,求
人,求 人中其中
人中其中 人为“酒后驾车”另
人为“酒后驾车”另 人为“醉酒驾车”的概率.
人为“醉酒驾车”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在每年的春节后,某市政府都会发动公务员参与到植树活动中去.为保证树苗的质量,该市林管部门在植树前,都会在植树前对树苗进行检测.现从甲乙两种树苗中各抽测了10株树苗的高度,量出树苗的高度如下(单位:厘米):
甲:
乙:
(1)根据抽测结果,完成答题卷中的茎叶图,并根据你填写的茎叶图,对甲、乙两种树苗的高度作比较,写出两个统计结论;
(2)设抽测的10株甲种树苗高度平均值为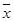 ,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的
,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的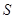 大小为多少?并说明
大小为多少?并说明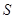 的统计学意义.
的统计学意义.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某学校100名学生期中考试语文成绩的频率分布直方图如下右图所示,其中成绩分组区间是: ,
,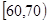 ,
, ,
,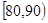 ,
, 。
。
求图中a的值;
根据频率分布直方图,估计这100名学生语文成绩的平均分;
若这100名学生语文成绩某些分数段的人数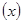 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数
之比如下表所示,求数学成绩在 之外的人数。
之外的人数。
| 分数段 |  | 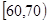 |  | 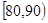 |
x :y :y | 1:1 | 2:1 | 3:4 | 4:5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某同学在生物研究性学习中,对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究,于是他在4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下资料:
| 日 期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 颗 颗 | 23 | 25 | 30 | 26 | 16 |
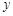 关于
关于 的线性回归方程
的线性回归方程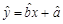 ;
;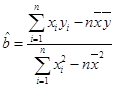
 ,
, )
)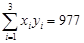 ,
, )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了估计某校的某次数学考试情况,现从该校参加考试的600名学生中随机抽出60名学生,其成绩(百分制)均在 上,将这些成绩分成六段
上,将这些成绩分成六段 ,
, ,…
,… ,后得到如图所示部分频率分布直方图.
,后得到如图所示部分频率分布直方图.
(1)求抽出的60名学生中分数在 内的人数;(5分)
内的人数;(5分)
(2)若规定成绩不小于85分为优秀,则根据频率分布直方图,估计该校优秀人数.(5分)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某高校组织的自主招生考试,共有1000名同学参加笔试,成绩均介于60分到100分之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分为4组:第1组[60,70),第2组[70,80),第3组[80,90),第4组[90,100].如图是按上述分组方法得到的频率分布直方图,且笔试成绩在85分(含85分)以上的同学有面试资格.
(Ⅰ)估计所有参加笔试的1000名同学中,有面试资格的人数;
(Ⅱ)已知某中学有甲、乙两位同学取得面试资格,且甲的笔试比乙的高;面试时,要求每人回答两个问题,假设甲、乙两人对每一个问题答对的概率均为 ;若甲答对题的个数不少于乙,则甲比乙优先获得高考加分资格.求甲比乙优先获得高考加分资格的概率.
;若甲答对题的个数不少于乙,则甲比乙优先获得高考加分资格.求甲比乙优先获得高考加分资格的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com