
| ��ʽ�±� | ��ʽ�±� | ŷʽ�±� | |
| 40�����ϣ���40�꣩Ա������ | 10 | y | 4 |
| 40������Ա������ | 2 | 6 | x |
| P��K2��k0�� | 0.1 | 0.01 | 0.01 |
| k0 | 2.706 | 6.635 | 10.828 |
���� ��1��������ɵã�$\left\{\begin{array}{l}{2+6+x=\frac{1}{3}��42}\\{10+y+4+2+6+x=42}\end{array}\right.$��������ɵó���
��2���ó������������ù�ʽ�����k�����ɵó����ۣ�
��3�����ֲ�����ķ�����Ա���������ȡ7�ˣ����������±��������±���ŷʽ�±�����ȡ���������ֱ�Ϊ��
2��3��2����Ǽס���2���б���ȡ��������X����ȡֵΪ��0��1��2�����ó����ηֲ��м��ɵó���
��� �⣺��1��������ɵã�$\left\{\begin{array}{l}{2+6+x=\frac{1}{3}��42}\\{10+y+4+2+6+x=42}\end{array}\right.$�����x=6��y=14��
��2��
| ��ŷʽ�±� | ŷʽ�±� | �ϼ� | |
| 40�����ϣ���40�꣩Ա������ | 24 | 4 | 28 |
| 40������Ա������ | 8 | 6 | 14 |
| �ϼ� | 32 | 10 | 42 |
| X | 0 | 1 | 2 |
| P | $\frac{10}{21}$ | $\frac{10}{21}$ | $\frac{1}{21}$ |
���� ���⿼���˶����Լ���ԭ���������ηֲ��м�����ѧ�������ֲ������������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
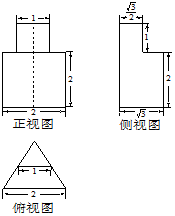
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{6}$ | B�� | $\frac{��}{4}$ | C�� | $\frac{��}{3}$ | D�� | $\frac{2��}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2lg5 | B�� | 0 | C�� | -1 | D�� | -2lg5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��a�� | B�� | ��0��b�� | C�� | ��0��$\sqrt{{a}^{2}+{b}^{2}}$�� | D�� | ��0��$\sqrt{ab}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ͼ�����$x=\frac{��}{3}$�Գ� | |
| B�� | ͼ�����$��\frac{2��}{3}��0��$�Գ� | |
| C�� | ��$[\frac{2��}{3}��\frac{8��}{3}]$�ϵ����ݼ� | |
| D�� | ��������������$[2k��-\frac{4��}{3}��2k��+\frac{2��}{3}]��k��Z��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
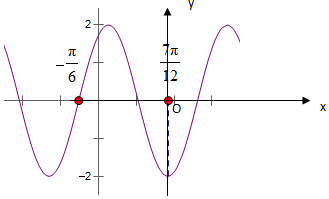 ��֪f��x��=Asin����x+�գ���A��0���أ�0��-�У��գ��У���ͼ����ͼ��ʾ��
��֪f��x��=Asin����x+�գ���A��0���أ�0��-�У��գ��У���ͼ����ͼ��ʾ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com