
【题目】已知数列{an}的前n项和Sn=kcn﹣k(其中c,k为常数),且a2=4,a6=8a3 .
(1)求an;
(2)求数列{nan}的前n项和Tn .
【答案】
(1)解:由Sn=kcn﹣k,得an=sn﹣sn﹣1=kcn﹣kcn﹣1; (n≥2),
由a2=4,a6=8a3.得kc(c﹣1)=4,kc5(c﹣1)=8kc2(c﹣1),解得 ![]() ;
;
所以a1=s1=2;
an=sn﹣sn﹣1=kcn﹣kcn﹣1=2n,(n≥2),
于是an=2n
(2)解:∵nan=n2n;
∴Tn=2+222+323+…+n2n;
2Tn=22+223+324+…+(n﹣1)2n+n2n+1;
∴﹣Tn=2+22+23…+2n﹣n2n+1= ![]() ﹣n2n+1=﹣2+2n+1﹣n2n+1;
﹣n2n+1=﹣2+2n+1﹣n2n+1;
即:Tn=(n﹣1)2n+1+2
【解析】(1)先根据前n项和求出数列的通项表达式;再结合a2=4,a6=8a3求出c,k,即可求出数列的通项;(2)直接利用错位相减法求和即可.
【考点精析】本题主要考查了等比数列的通项公式(及其变式)和数列的前n项和的相关知识点,需要掌握通项公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系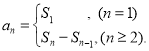 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】若定义在R上的偶函数f(x)满足f(x﹣1)=f(x+1).且当x∈[﹣1,0]时,f(x)=﹣x2+1,如果函数g(x)=f(x)﹣a|x|恰有8个零点,则实数a的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log ![]() (
( ![]() )满足f(﹣2)=1,其中a为实常数.
)满足f(﹣2)=1,其中a为实常数.
(1)求a的值,并判定函数f(x)的奇偶性;
(2)若不等式f(x)>( ![]() )x+t在x∈[2,3]上恒成立,求实数t的取值范围.
)x+t在x∈[2,3]上恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,椭圆![]() :
: ![]() (
(![]() )的离心率为
)的离心率为![]() ,左焦点为
,左焦点为![]() ,右焦点为
,右焦点为![]() ,短轴两个端点
,短轴两个端点![]() 、
、![]() ,与
,与![]() 轴不垂直的直线
轴不垂直的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,记直线
,记直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,且
,且![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)求证直线![]() 与
与![]() 轴相交于定点,并求出定点坐标;
轴相交于定点,并求出定点坐标;
(3)当弦![]() 的中点
的中点![]() 落在
落在![]() 内(包括边界)时,求直线
内(包括边界)时,求直线![]() 的斜率的取值.
的斜率的取值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小图给出了某池塘中的浮萍蔓延的面积![]() 与时间
与时间![]() (月)的关系的散点图.有以下叙述:
(月)的关系的散点图.有以下叙述:

①与函数![]() 相比,函数
相比,函数![]() 作为近似刻画
作为近似刻画![]() 与
与![]() 的函数关系的模型更好;
的函数关系的模型更好;
②按图中数据显现出的趋势,第![]() 个月时,浮萍的面积就会超过
个月时,浮萍的面积就会超过![]() ;
;
③按图中数据显现出的趋势,浮萍每个月增加的面积约是上个月增加面积的两倍;
④按图中数据显现出的趋势,浮萍从![]() 月的
月的![]() 蔓延到
蔓延到![]() 至少需要经过
至少需要经过![]() 个月.
个月.
其中正确的说法有__________(填序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)若点![]() ,在
,在![]() 中按均匀分布出现.
中按均匀分布出现.
(1)点![]() 横、纵坐标分别由掷骰子确定,第一次确定横坐标,第二次确定纵坐标,则点
横、纵坐标分别由掷骰子确定,第一次确定横坐标,第二次确定纵坐标,则点![]() 落在上述区域的概率?
落在上述区域的概率?
(2)试求方程![]() 有两个实数根的概率.
有两个实数根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=kax﹣a﹣x(a>0且a≠1)在(﹣∞,+∞)上既是奇函数又是增函数,则函数g(x)=loga(x+k)的图象是( )
A.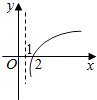
B.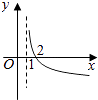
C.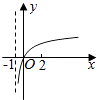
D.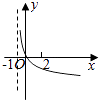
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】奥地利遗传学家孟德尔1856年用豌豆作实验时,他选择了两种性状不同的豌豆,一种是子叶颜色为黄色,种子性状为圆形,茎的高度为长茎,另一种是子叶颜色为绿色,种子性状为皱皮,茎的高度为短茎。我们把纯黄色的豌豆种子的两个特征记作![]() ,把纯绿色的豌豆的种子的两个特征记作
,把纯绿色的豌豆的种子的两个特征记作![]() ,实验杂交第一代收获的豌豆记作
,实验杂交第一代收获的豌豆记作![]() ,第二代收获的豌豆出现了三种特征分别为
,第二代收获的豌豆出现了三种特征分别为![]() ,
,![]() ,
,![]() ,请问,孟德尔豌豆实验第二代收获的有特征
,请问,孟德尔豌豆实验第二代收获的有特征![]() 的豌豆数量占总收成的( )
的豌豆数量占总收成的( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com