
 的周期为
的周期为 ,图象的一个对称中心为
,图象的一个对称中心为 ,将函数
,将函数 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个 单位长度后得到函数
单位长度后得到函数 的图象。
的图象。 与
与 的解析式
的解析式 ,使得
,使得 按照某种顺序成等差数列?若存在,请确定
按照某种顺序成等差数列?若存在,请确定 的个数,若不存在,说明理由;
的个数,若不存在,说明理由; 与正整数
与正整数 ,使得
,使得 在
在 内恰有2013个零点
内恰有2013个零点
 (Ⅱ)存在(Ⅲ)当
(Ⅱ)存在(Ⅲ)当 ,
, 时,函数
时,函数 在
在 内恰有
内恰有 个零点
个零点 的周期为
的周期为 ,
, ,得
,得
 的一个对称中心为
的一个对称中心为 ,
,
 ,得
,得 ,所以
,所以
 图象上所有点的横坐标伸长到原来的
图象上所有点的横坐标伸长到原来的 倍(纵坐标不变)后可得
倍(纵坐标不变)后可得 的图象,再将
的图象,再将 的图象向右平移
的图象向右平移 个单位长度后得到函数
个单位长度后得到函数
 时,
时, ,
,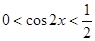

 在
在 内是否有解
内是否有解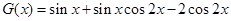 ,
,

 ,所以
,所以 ,
, 在
在 内单调递增
内单调递增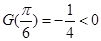 ,
,
 的图象连续不断,故可知函数
的图象连续不断,故可知函数 在
在 内存在唯一零点
内存在唯一零点 ,
, 满足题意
满足题意 ,令
,令
 ,即
,即 时,
时, ,从而
,从而 不是方程
不是方程 的解,所以方程
的解,所以方程 等价于关于
等价于关于 的方程
的方程 ,
,
 时方程解的情况
时方程解的情况 ,
,
 与曲线
与曲线 在
在 的交点情况
的交点情况 ,令
,令 ,得
,得 或
或
 变化时,
变化时, 和
和 变化情况如下表
变化情况如下表 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  | 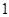 |  |  |  |  |
 且
且 趋近于
趋近于 时,
时, 趋向于
趋向于
 且
且 趋近于
趋近于 时,
时, 趋向于
趋向于
 且
且 趋近于
趋近于 时,
时, 趋向于
趋向于
 且
且 趋近于
趋近于 时,
时, 趋向于
趋向于
 时,直线
时,直线 与曲线
与曲线 在
在 内有无交点,在
内有无交点,在 内有
内有 个交点;
个交点; 时,直线
时,直线 与曲线
与曲线 在
在 内有
内有 个交点,在
个交点,在 内无交点;
内无交点; 时,直线
时,直线 与曲线
与曲线 在
在 内有
内有 个交点,在
个交点,在 内有
内有 个交点
个交点 的周期性,可知当
的周期性,可知当 时,直线
时,直线 与曲线
与曲线 在
在 内总有偶数个交点,从而不存在正整数
内总有偶数个交点,从而不存在正整数 ,使得直线
,使得直线 与曲线
与曲线 在
在 内恰有
内恰有 个交点;当
个交点;当 时,直线
时,直线 与曲线
与曲线 在
在 内有
内有 个交点,由周期性,
个交点,由周期性, ,所以
,所以
 ,
, 时,函数
时,函数 在
在 内恰有
内恰有 个零点
个零点

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源:不详 题型:单选题
 )sin(
)sin( )的单调递增区间为( )
)的单调递增区间为( ) | A.[(2k+1)π,2(k+1)π] | B.[(k+ )π,(k+1)π] )π,(k+1)π] |
C.[kπ,(k+ ) π] ) π] | D.[2kπ, (2k+1)π] |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,给出下列命题:
,给出下列命题: 的图象关于直线
的图象关于直线 对称;②函数
对称;②函数 的图象可由
的图象可由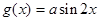 的图象向左平移
的图象向左平移 个单位而得到;③把函数
个单位而得到;③把函数 的图象上的所有点的纵坐标保持不变,横坐标缩短到原来的
的图象上的所有点的纵坐标保持不变,横坐标缩短到原来的 倍,可以得到函数
倍,可以得到函数 )的图象;④若函数
)的图象;④若函数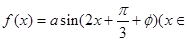 R)为偶函数,则
R)为偶函数,则 .其中正确命题的序号有 ;(把你认为正确的命题的序号都填上)。
.其中正确命题的序号有 ;(把你认为正确的命题的序号都填上)。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com