
分析 (1)由已知等式变形得到${a_{n+1}}-{a_n}=1(n≥2,n∈{N^*})$,根据等差数列的定义得到证明并且求通项公式;
(2)由(1)得到数列$\{\frac{1}{{{a_n}{a_{n+1}}}}\}$的通项公式,利用裂项求和即可得到Tn.
解答 解:(1)证明:由已知,${a_{n+1}}-{a_n}=1(n≥2,n∈{N^*})$,且a2-a1=1,
∴数列{an}是以a1=2为首项,公差为1的等差数列,∴an=n+1.…(6分)
(2)$\frac{1}{{{a_n}{a_{n+1}}}}=\frac{1}{(n+1)(n+2)}=\frac{1}{n+1}-\frac{1}{n+2}$.${T_n}=\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{n+1}-\frac{1}{n+2}=\frac{1}{2}-\frac{1}{n+2}=\frac{n}{2(n+2)}$.…(12分)
点评 本题考查了等差数列的证明、通项公式的求法以及裂项求和;属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
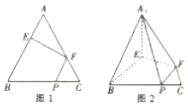 在边长为3的正三角形ABC中,E,F,P分别是AB,AC,BC边上的点,满足$\frac{AE}{EB}$=$\frac{CF}{FA}$=$\frac{CP}{PB}$=$\frac{1}{2}$,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连结A1B,A1P(如图),则以下结论错误的是( )
在边长为3的正三角形ABC中,E,F,P分别是AB,AC,BC边上的点,满足$\frac{AE}{EB}$=$\frac{CF}{FA}$=$\frac{CP}{PB}$=$\frac{1}{2}$,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连结A1B,A1P(如图),则以下结论错误的是( )| A. | CF∥平面A1EP | |
| B. | A1E⊥平面BEP | |
| C. | 点B到面A1PF的距离为$\sqrt{3}$ | |
| D. | 异面直线BP与A1F所成角的余弦值为$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com