
【题目】如图,在三棱柱![]() 中,
中,![]() ⊥底面
⊥底面![]() ,底面
,底面![]() 为等边三角形,
为等边三角形,![]() ,
,![]() ,
, ![]() ,
,![]() 分别为
分别为![]() ,
, ![]() 的中点.
的中点.
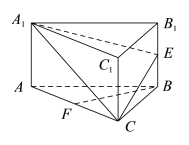
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成二面角的余弦值;
所成二面角的余弦值;
(3)设平面![]() 与平面
与平面![]() 的交线为
的交线为![]() 求证:
求证:![]() 与平面
与平面![]() 不平行.
不平行.
【答案】(1)证明见解析;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)法一:取![]() 中点
中点![]() ,连接
,连接![]() ,证明四边形
,证明四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,即可证明;法二:取
,即可证明;法二:取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,因为
,因为![]() 为平行四边形,所以
为平行四边形,所以![]() ,证明平面
,证明平面![]() 平面
平面![]() 延长
延长![]() 交于点
交于点![]() ,连接
,连接![]() ,在
,在![]() 中,
中,![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,![]()
(2)求出平面A1EC的法向量和平面ABC的法向量,利用向量法能求出平面A1EC与平面ABC所成二面角的余弦值.
(3)法一:反证法,推得![]() ,与
,与![]() 相交矛盾;法二:延长
相交矛盾;法二:延长![]() 交于点
交于点![]() ,连接
,连接![]() ,得到两平面的交线
,得到两平面的交线![]() ,
,![]() ,所以
,所以![]() 与平面
与平面![]() 不平行.
不平行.
(1)证法1:
取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() 且
且![]() ,又
,又![]() 且
且![]()
所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,
,
又![]() 平面
平面![]()
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
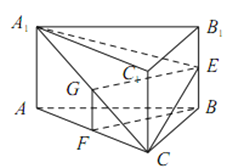
证法2:取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
因为![]() 为平行四边形,所以
为平行四边形,所以![]() ,
,![]() ,
,
所以平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
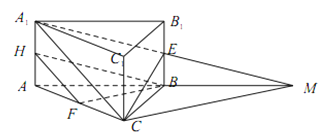
证法3:延长![]() 交于点
交于点![]() ,连接
,连接![]() ,
,
在![]() 中,
中,![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
又![]() 平面
平面![]()
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)因为![]() 底面
底面![]() ,
,![]() ,
,
所以![]() 底面
底面![]() ,
,
又三角形![]() 为等边三角形,
为等边三角形,![]() 为
为![]() 中点,所以
中点,所以![]() ,
,
以![]() 为原点,建立如图所示所示的坐标系,
为原点,建立如图所示所示的坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则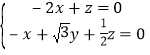 ,
,
令![]() ,则
,则![]() ,
,![]() ,
,
易知平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则![]() ,
,
由图可知,所求二面角为锐角,所以二面角的余弦值为![]() .
.

(3)方法1:
假设![]() 与平面
与平面![]() 平行,
平行,
因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,所以
,所以![]() ,
,
同理![]() ,
,
所以![]() ,与
,与![]() 相交矛盾,
相交矛盾,
所以![]() 与平面
与平面![]() 不平行.
不平行.
方法2:延长![]() 交于点
交于点![]() ,连接
,连接![]() ,则
,则![]() 就是直线
就是直线![]() ,
,
![]() ,所以
,所以![]() 与平面
与平面![]() 不平行.
不平行.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为自然对数的底数),
为自然对数的底数),![]() 是
是![]() 的导函数.
的导函数.
(Ⅰ)当![]() 时,求证
时,求证![]() ;
;
(Ⅱ)是否存在正整数![]() ,使得
,使得![]() 对一切
对一切![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,短轴长为4.
,短轴长为4.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作两条直线,分别交椭圆
作两条直线,分别交椭圆![]() 于
于![]() 两点(异于
两点(异于![]() ),当直线
),当直线![]() ,
,![]() 的斜率之和为4时,直线
的斜率之和为4时,直线![]() 恒过定点,求出定点的坐标.
恒过定点,求出定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,以棱长为1的正方体的具有公共顶点的三条棱所在直线为坐标轴,建立空间直角坐标系Oxyz,点P在对角线AB上运动,点Q在棱CD上运动.
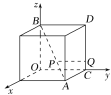
(1)当P是AB的中点,且2|CQ|=|QD|时,求|PQ|的值;
(2)当Q是棱CD的中点时,试求|PQ|的最小值及此时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用“算筹”表示数是我国古代计数方法之一,计数形式有纵式和横式两种,如图1所示.金元时期的数学家李治在《测圆海镜》中记载:用“天元术”列方程,就是用算筹来表示方程中各项的系数.所谓“天元术”,即是一种用数学符号列方程的方法,“立天元一为某某”,意即“设![]() 为某某”.如图2所示的天元式表示方程
为某某”.如图2所示的天元式表示方程![]() ,其中
,其中![]() 表示方程各项的系数,均为筹算数码,在常数项旁边记一“太”字或在一次项旁边记一“元”字,“太”或“元”向上每层减少一次幂,向下每层增加一次幂.试根据上述数学史料,判断图3所示的天元式表示的方程是________________
表示方程各项的系数,均为筹算数码,在常数项旁边记一“太”字或在一次项旁边记一“元”字,“太”或“元”向上每层减少一次幂,向下每层增加一次幂.试根据上述数学史料,判断图3所示的天元式表示的方程是________________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com